60° Angle And Importance of Being The Other End of a Diameter
What Is This About?
Source
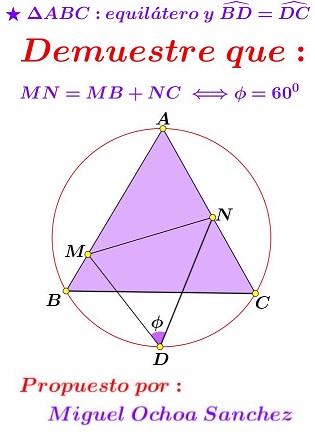
Problem
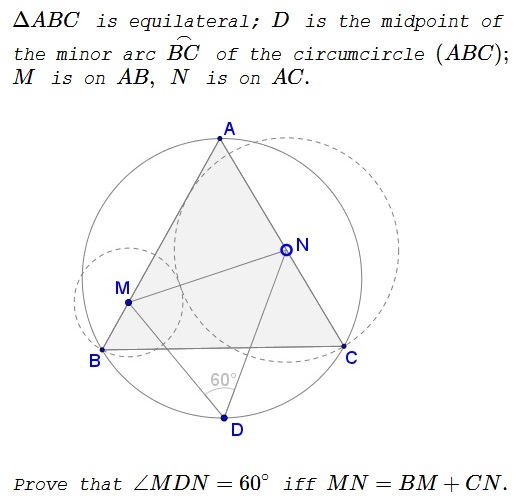
Solution 1
Observe that $AD\,$ is a diameter of $(ABC).\,$ It follows that $\angle ACD=\angle ABD=90^{\circ}.\,$ Also, $\angle CDB=120^{\circ}.\,$
$\mathbf{MN=BM+CN\,\Rightarrow\,\angle MDN=60^{\circ}}$
Let $G\in MN\,$ be such that $DG\perp MN.\,$ Consider circles $(M)=C(M,B)\,$ and $(N)=C(N,C).\,$

To satisfy $MN=BM+CN,\,$ the two circles need to pass through $G\,$ where they touch each other, such that $BM=GM\,$ and $CN=GN.\,$ Note that the four triangles $BDM,\,$ $GDM,\,$ $GDN,\,$ and $CDN\,$ are right.
$BM=GM\,$ and $CN=GN\,$ is equivalent to
$\qquad\qquad\Delta BMD=\Delta GMD\,$ and $\Delta CND=\Delta GND$
which is equivalent to
$\qquad\qquad\angle BDM=\angle GDM\,$ and $\angle CDN=\angle GDN$
which implies
$\qquad\qquad\angle GDM+\angle GDN=60^{\circ}.$
$\mathbf{\angle MDN=60^{\circ}\,\Rightarrow\,MN=BM+CN}$
Consider circle $(D)\,$ through $B\,$ and $C.\,$ Let a tangent from $M\,$ to $(D)\,$ cross $AC\,$ at $N',\,$ with $G\,$ the tangency point.
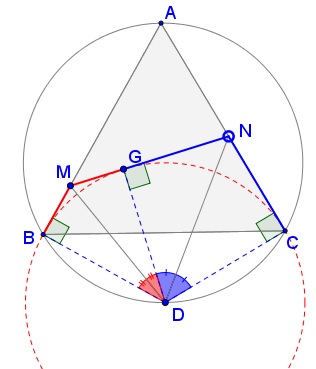
Then, $BM=GM\,$ and $CN'=GN',\,$ implying as above, that $\angle MDN'=60^{\circ}.\,$ It follows that $N'=N,\,$ $MN\,$ is tangent to $(D)\,$ at $G;\,$ $BM=GM\,$ and $CN=GN,\,$ and, therefore, $MN=BM+CN.$
Solution 2
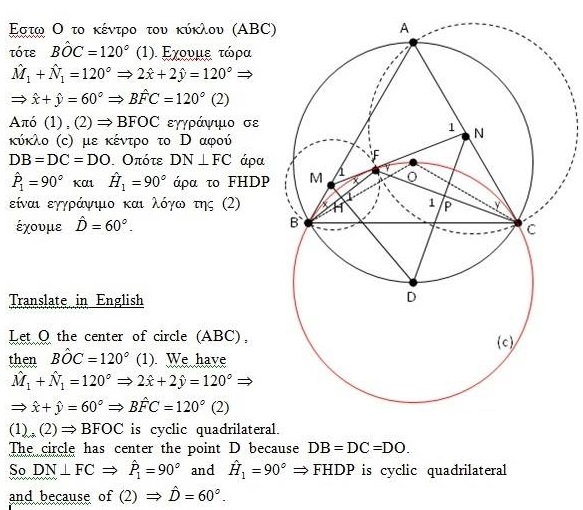
Acknowledgment
The above problem by Miguel Ochoa Sanchez was originally posted at the Peru Geometrico facebook group and appeared on my timeline. Solution 2 is by Stelios Karpathios and was been translated and posted by Takis Chronopoulos.
Thanos Kalogerakis has observed that the statement holds for isosceles triangles $ABC,\,$ with $AB=AC\,$ and $\displaystyle \angle MDN=\frac{1}{2}(180^{\circ}-\angle ABC).\,$ The proof appears to require only minor modifications.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73607172
