One More Property of Equilateral Triangles
What Is This About?
Source
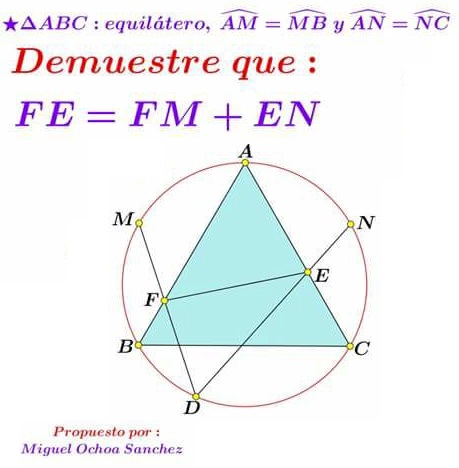
Problem

Solution
Let $O\,$ be the center of $(ABC).\,$ Then, not only $OM\perp AB\,$ and $ON\perp AC,\,$ but $OM\,$ and $ON\,$ are divided in half by the points of intersection.

This makes triangles $OFM\,$ and $OEN\,$ isosceles so that $FM=FO\,$ and $EN=NO.\,$ Suffice it to show that $O\in EF.$ This is achieved by angle chasing.
$\displaystyle \begin{align} \angle MDN&=60^{\circ},\\ \angle AFM&=\frac{1}{2}(\overset{\frown}{AM}+\overset{\frown}{BD}),\\ \angle AEN&=\frac{1}{2}(\overset{\frown}{AN}+\overset{\frown}{CD}),\\ \angle AFM+\angle AEN&=\frac{1}{2}(2\cdot 60^{\circ}+(\overset{\frown}{BD}+\overset{\frown}{CD})),\\ &=120^{\circ},\\ \angle OFM+\angle OEN&=2(\angle AFM+\angle AEN)=240^{\circ},\\ \angle OFD+\angle OED&=360^{\circ}-2(\angle AFM+\angle AEN)=120^{\circ}. \end{align}$
It follows that $\angle OFD+\angle OED+\angle EDF=180^{\circ},\,$ because $\angle EDF=\angle MDN,\,$ which makes $EOF\,$ a straight line.
Acknowledgment
The above problem was kindly posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73562851
