When Is Triangle Equilateral:
Miguel Ochoa Sanchez's Criterion
Source
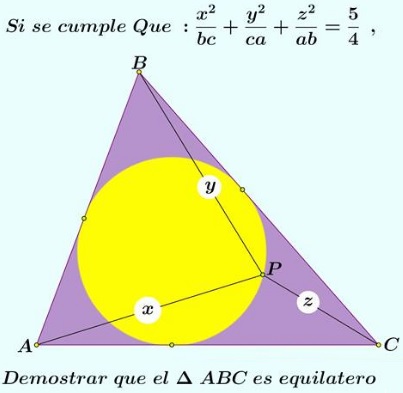
Problem
Let $P\;$ be a point on the incircle of $\Delta ABC.\;$ Let $x,y,z\;$ be the distances of $P\;$ to the vertices $A,B,C.\;$ Prove that if
$\displaystyle \frac{x^2}{bc}+\frac{y^2}{ca}+\frac{z^2}{ab}=\frac{5}{4}$
then the triangle is equilateral.
Proof
First observe that the identity in the problem is equivalent to $\displaystyle ax^2+by^2+cz^2=\frac{5}{4}abc.\;$ Now, using the barycentric coordinates, the circle with center $M(u,v,w),\;$ $u+v+w=1,\;$ and radius $r,\;$ has the equation
$ux^2+vy^2+wz^2 = r^2+a^2vw+b^2wu+c^2uv.$
With this in mind, the incircle is described by
$\displaystyle \begin{align}\frac{1}{a+b+c}\left(ax^2+by^2+cz^2\right)&=r^2+\frac{1}{(a+b+c)^2}(a^2bc+ab^2c+abc^2)\\ &=r^2+\frac{abc}{a+b+c}. \end{align}$
Thus the problem reduces to showing that
$\displaystyle r^2(a+b+c)+abc=\frac{5}{4}abc,$
which is the same as
$4r^2(a+b+c)=abc.$
However, $abc=4RS,\;$ where $R\;$ is the circumradius and $S\;$ the area of $\Delta ABC.\;$ If $s\;$ is the semiperimeter of the triangle then $rs=S\;$ and $4r^2(a+b+c)=8rS,\;$ meaning that the identity is equivalent to $2r=R,\;$ which only holds for the equilateral triangle.
Acknowledgment
The problem, due to Miguel Ochoa Sanchez, has been kindly posted by Leo Giugiuc at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73612365
