Graphing Equations Is Useful, II

We already looked into a problem offered at the 1957 (XX) Moscow Mathematical Olympiad to the 8th graders. Here is a more difficult one that was given to high school seniors:

For \(n\gt 0\), find all real solutions of the system

\( \begin{array}{3,5} 1-x_{1}^{2}&=x_{2}, \\ 1-x_{2}^{2}&=x_{3}, \\ \cdots\cdots\cdots & \\ 1-x_{n-1}^{2}&=x_{n}, \\ 1-x_{n}^{2}&=x_{1}, \end{array} \)

Solution

For \(n\gt 0\), find all real solutions of the system

\( \begin{array}{3,5} 1-x_{1}^{2}&=x_{2}, \\ 1-x_{2}^{2}&=x_{3}, \\ \cdots\cdots\cdots & \\ 1-x_{n-1}^{2}&=x_{n}, \\ 1-x_{n}^{2}&=x_{1}, \end{array} \)

It is rather obvious that the system represent iterations of function \(\displaystyle f(x)=1-x^{2}\) and the question is to find a starting point \(x_{1}\) to which the iterations return after \(n\) applications of function \(f\). Let's graph \(y=f(x)\). (The straight line is the graph of \(y=x\).)

graph of the function y= 1-x^2

Obviously, there are two solutions defined by \(f(x)=x\). Solving the quadratic equation we obtain two stationary points of function \(f\):

\( \displaystyle \frac{-1\pm\sqrt{5}}{2} \)

On the graph these correspond to points A\(\space=\left(\displaystyle\frac{-1+\sqrt{5}}{2},\displaystyle\frac{-1+\sqrt{5}}{2}\right)\) and B\(\space=\left(\displaystyle\frac{-1-\sqrt{5}}{2},\displaystyle\frac{-1-\sqrt{5}}{2}\right)\).

Obviously this gives two sets of solutions for any \(n\gt 0\), but this is not the whole story. If \(n\) is even there are two more solutions: starting with \(x_{1}=0\) and the other with \(x_{1}=1\). In both cases the \(0\)s and \(1\)s then alternate. Are there any other solutions? The answer is No, but I am not sure how the high schoolers were supposed to prove that. The graph provides some clues, though.

By the construction, \((x_{1},x_{2})\) is a point on the graph of \(y=f(x)\), as is any pair of successive iterations. The diagram above shows how two points \((x_{1},x_{2})\) and \((x_{2},x_{3})\) are connected graphically. There is an "intermediate" point \((x_{2},x_{2})\) that lies on the diagonal \(y=x\). This observation helps to realize that, for a solution to exist, \(x_{1}\) could not be outside the interval \(\left(\displaystyle\frac{-1-\sqrt{5}}{2},\displaystyle\frac{1+\sqrt{5}}{2}\right)\). If it is, the iteration will certainly diverge to \(\displaystyle -\infty\).

The applet below illustrates the behavior of the iterations in general. Click in the applet area to reset the initial value of \(x_{1}\).

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Wherever you start in the interval \(\left(\displaystyle\frac{-1-\sqrt{5}}{2},\displaystyle\frac{1+\sqrt{5}}{2}\right)\), the iteration settle into the 2-loop: \(1,0,1,0,\ldots\). It helps to consider the graph of the iterated function \(f(f(x))=1-(1-x^{2})^{2}=x^{2}(2-x^{2})\):

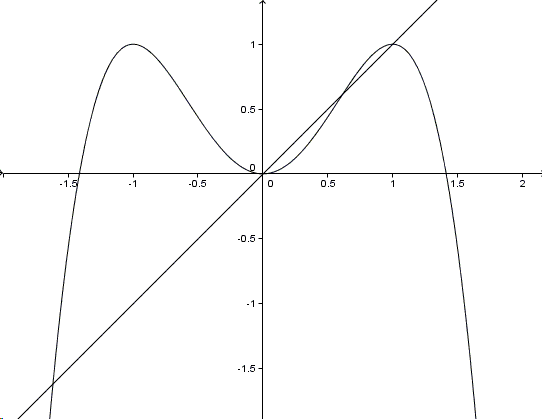
graph of the function y= x^2*(2-x^2)

The iterated function has four stationary points: \(0\) and \(1\) are attractive, while \(\displaystyle\frac{-1\pm\sqrt{5}}{2}\) are repelling. It may also help to graph the next two iterates:

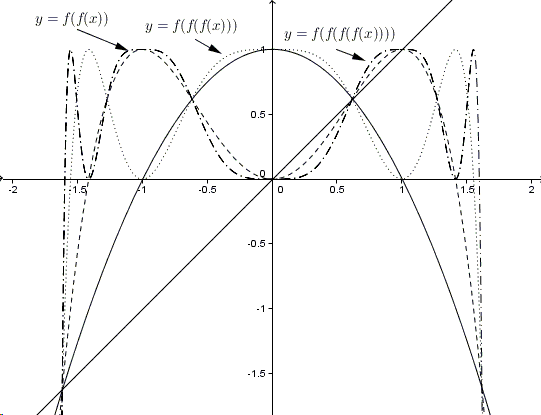
graph of the the first four iterates

No additional stationary points seem to appear (some would if there were other loops, i.e., solutions to the system for some \(n\)). By contrast, for the iterates of another quadratic function \(y=4x(1-x)\), new stationary points pop up all the time:

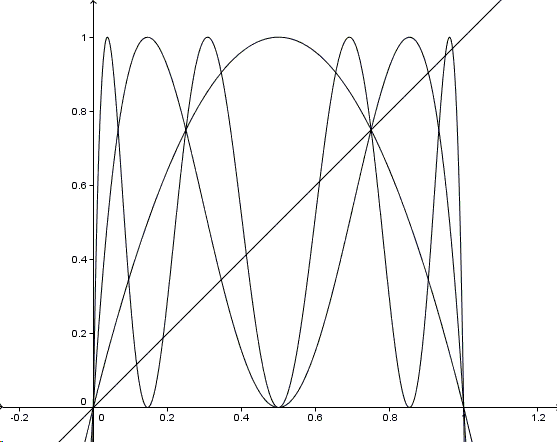
graph of the the first four iterates for 4x(1-x)

Why not for \(y=1-x^2\)? To answer this question we have to prove that if \(x\ne 1-x^2\) then also \(x\ne 1-(1-x^{2})^{2}\). Let's do that. One will have to consider several cases. I shall point out to just one. Let \(\alpha=(-1+\sqrt{5})/2\). One can see it from the graphs that, say, for \(0\lt x\lt\alpha\), \(x\lt 1-x^{2}\), but \(x\gt 1-(1-x^{2})^{2}\gt 0\). As a consequence, \(0\lt 1-(1-x^{2})^{2} \lt \alpha\) so that to this iterate applies whatever applied to \(x\). Thus no new stationary points may appear in the interval \((0,\alpha)\).

Hopefully, the remaining cases could be dealt with similarly.

Systems of Iterated Equations

71925088