Parallelogram and Four Equilateral Triangles

Consider triangles $GAH$ and $GDI.$

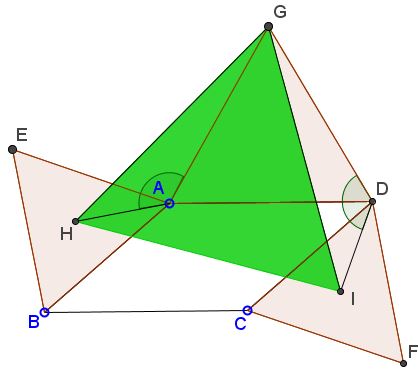
Certainly, $GA=GD$ and $AH=DI.$ Also, let $\angle ABC=\alpha.$ Then

$\begin{align} \angle GAH &=360^{\circ}-(180^{\circ}-\alpha)-60^{\circ}-30^{\circ}=90^{\circ}+\alpha,\\ \angle GDI &=\alpha +60^{\circ}+30^{\circ}=90^{\circ}+\alpha. \end{align}$

So that the two angles, and, therefore, the two triangles are equal. In particular, $\angle AGH=\angle DGI,$ implying

$\angle HGI = \angle AGD +\angle AGH -\angle DGI=\angle AGD=60^{\circ}.$

Since $GH=GI,$ $\Delta GHI$ is isosceles with the apex angle of $60^{\circ},$ so it in fact is equilateral.