Pairs of Areas in Equilateral Triangle

Solution

References

1. B. J. McCartin, An Elementary Property of the Equilateral Triangle: A Tale of Two Proofs, International Mathematical Forum, Vol. 6, 2011, no. 14, 699 - 701

|Contact| |Front page| |Contents| |Geometry| |Eye opener|

Copyright © 1996-2018 Alexander Bogomolny

Solution

One solution is based on the following observation. There are three pairs of regions whose total area we seek to determine. The area of the circumcircle of the given equilateral triangle is thus split into three pairs of areas in question and the incircle.

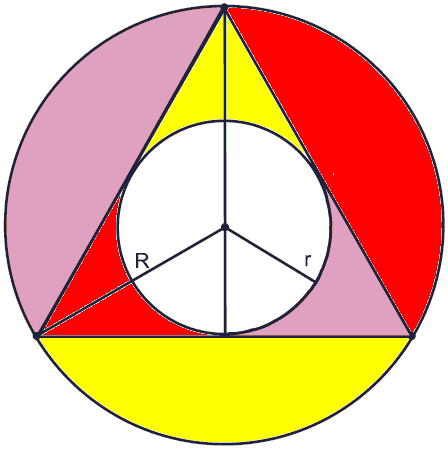
Let the area in question be S, A_R = πR² the area of the circumcircle, and A_r = πr² the area of the incircle.

3S + A_r = A_R.

In the equilateral triangle R = 2r. This is so because, in an equilateral triangle, the same lines serve as altitudes, medians, angle and perpendicular bisectors; while the same point serves as the centroid, incenter, and circumcenter. The centroid cuts the median in ratio 2:1. The "2" part is the circumradius, the "1" part is the inradius. Therefore,

3S = 4A_r - A_r = 3A_r,

and, finally, S = A_r, as required.

Related material Read more...
	Equilateral Triangles on Sides of a Quadrilateral
	Euler Line Cuts Off Equilateral Triangle
	Four Incircles in Equilateral Triangle
	Problem in Equilateral Triangle
	Problem in Equilateral Triangle II
	Sum of Squares in Equilateral Triangle
	Triangle Classification
	Isoperimetric Property of Equilateral Triangles
	Maximum Area Property of Equilateral Triangles
	Angle Trisectors on Circumcircle
	Equilateral Triangles On Sides of a Parallelogram
	Pompeiu's Theorem
	Circle of Apollonius in Equilateral Triangle

|Contact| |Front page| |Contents| |Geometry| |Eye opener|

Copyright © 1996-2018 Alexander Bogomolny