Spiral Similarity Leads to Equilateral Triangle
What Might This Be About?
Problem
In $\Delta ABC,$ right triangles $ABD$ and $ACE$ erected outwardly satisfy $\angle ABD=\angle ACE =30^{\circ}$ and $\angle BAD=\angle CAE = 90^{\circ};$ isosceles $BCF$ (erected inwardly) has base angles of $30^{\circ}.$
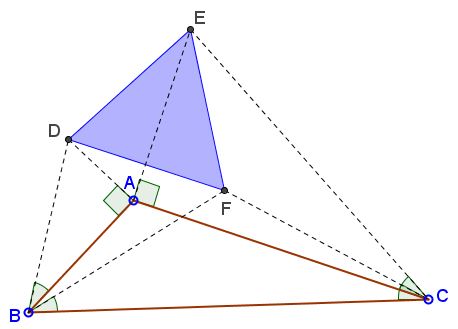
Prove that $\Delta DEF$ is equilateral.
Note that an equal triangles is obtained when the words "inwardly" and "outwardly" interchanged:
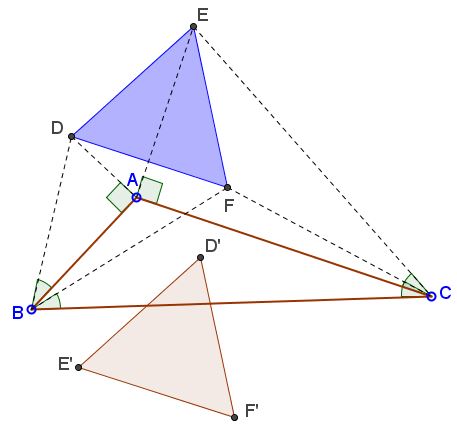
Solution 1
Complex numbers afford a straightforward solution.
Let's place the origin at $B$ and assume that $A$ and $C$ correspond to complex numbers $\alpha$ and $2\beta .$ $D$ is obtained from $A$ by a spiral similarity $\displaystyle\gamma=1+i\frac{\sqrt{3}}{3}$ around $B,$ and in the same way $F$ is obtained from $\alpha.$ $D$ is the image of $A$ under the (conjugate) spiral similarity $\displaystyle\overline{\gamma}=1-i\frac{\sqrt{3}}{3}$ around $C:$ $D=\gamma\alpha,$ $F=\gamma\beta,$ $E=2\beta +\overline{\gamma}(\alpha -2\beta ).$
A triangle with vertices $D$, $E,$ $F$ is equilateral if either $E+jD+j^{2}F=0$ or $E+j^{2}D+jF=0,$ where $j$ is a rotation through $120^{\circ}:$ $\displaystyle j=-\frac{1}{2}+i\frac{\sqrt{3}}{2},$ $\displaystyle \overline{j}=j^{2}=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.$
Easy calculations show that
$\displaystyle \gamma\cdot j=(1+i\frac{\sqrt{3}}{3})(-\frac{1}{2}+i\frac{\sqrt{3}}{2})=-1+i\frac{\sqrt{3}}{3}$
and
$\displaystyle \gamma\cdot \overline{j}=(1+i\frac{\sqrt{3}}{3})(-\frac{1}{2}-i\frac{\sqrt{3}}{2})=-i\frac{2\sqrt{3}}{3}.$
From here,
$\begin{align}\displaystyle E+jF&+j^{2}D = [2\beta +\overline{\gamma}(\alpha -2\beta )]+\gamma\alpha j +\gamma\beta\overline{j}\\ &=2\beta +(1-i\frac{\sqrt{3}}{3})(\alpha -2\beta )+(-1+i\frac{\sqrt{3}}{3})\alpha+(-i\frac{2\sqrt{3}}{3})\beta\\ &=\alpha(1-i\frac{\sqrt{3}}{3}-1+i\frac{\sqrt{3}}{3}) + \beta(2-2+i\frac{2\sqrt{3}}{3}-i\frac{2\sqrt{3}}{3}) = 0. \end{align}$
Solution 2
Let $M$ be the midpoint of $BC.$ We have $\angle ABD=\angle FBM = 30^{\circ}$ and $\angle BAD =\angle BMF =90^{\circ}.$ Also, $\Delta BAD \sim \Delta BMF,$ so $\displaystyle\frac{BD}{BF}=\frac{BA}{BM}.$ And, since $\angle ABD =\angle FBM,$ $\angle FBD =\angle MBA.$ From the proportion and angle equality we get $\Delta BDF \sim \Delta BAM,$ so $\displaystyle DF=\frac{BF\cdot AM}{BM}.$ Similarly, $\displaystyle EF =\frac{CF\cdot AM}{CM}.$ But $BF=CF$ and $BM=CM$ so it follows that $DF = EF.$
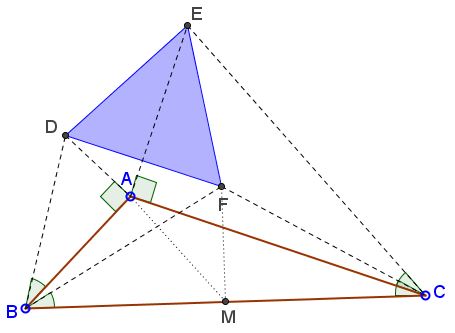
Additionally, $\angle BFD =\angle BMA,$ $\angle CFE =\angle CMA,$ so
$\begin{align} \angle DFE &= 360^{\circ} - (\angle BFC + \angle BFD + \angle CFE)\\ &= 360^{\circ} - (120^{\circ} + \angle BMF + \angle CMF)\\ &= 360^{\circ} - (120^{\circ} + 180^{\circ})\\ &=60^{\circ}, \end{align}$
from which we can already deduce $\Delta DEF$ is equilateral.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. The second solution is by Wojtek Wawrów
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73558974
