Miguel Ochoa's van Schooten Like Theorem
What Might This Be About?
10 May 2015, Created with GeoGebra
Problem
In $\Delta ABC,$ circle $(O)$ through $A$ and tangent to $BC$ in $D$ cuts $AB$ and $AC$ in $E$ and $F,$ respectively.
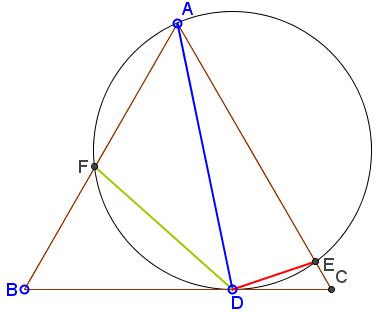
Prove that $AD = DE + DF.$
In the notations I follow the original formulation:
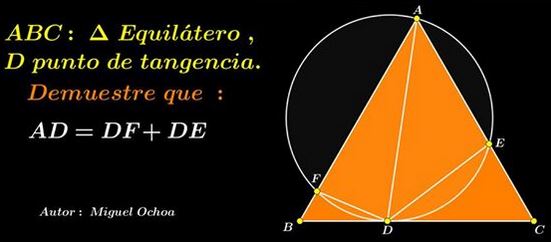
Proof 1
Rotate $A,B,C,F$ $60^{\circ}$ counterclockwise around $D$ into positions $A',B',C',F',$ respectively.
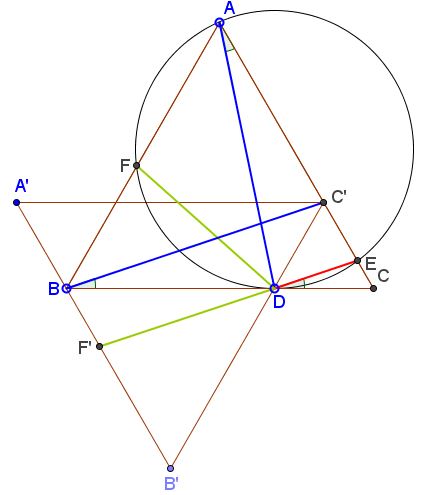
Since $\angle EDF=120^{\circ},$ $F'$ is collinear with $D$ and $E$ so that
$\begin{align} EF'&=DE+DF'\\ &=DE+DF. \end{align}$
I am going to show that
$BC'=AD,$
$BC'\parallel EF'.$
Since, obviously, $A'B'\parallel AC,$ this will furnish the proof of the statement.
$CC'=CD,$ implying $BD=AC'.$ Also, $\angle BDC=\angle AC'D=120^{\circ}.$ It follows that triangles $BC'D$ and ADC' are equal, so that, in particular, $BC'=AD.$ In addition, $\angle C'BD=\angle DAC'.$ But $\angle DAC'=\angle DAC=\angle CDE,$ the former being an inscribed angle subtended by the arc $DE,$ the latter is defined by the chord $DE$ and the tangent at $D.$ Thus, $\angle C'BD=\angle EDC,$ making $BC'\parallel DE$ and, hence, $BC'\parallel EF'.$
Proof 2
Without loss of generality, set $AB=1,$ $BD=k$ and $CD=1-k,$ where $k\in(0,1).$ By the Power of a Point Theorem, $BF\cdot AB=BD^{2},$ implying $BF=k^{2}$ and $AF=1-k^2.$ By Stewart's theorem in $\Delta ABD$ and the cevian $DF,$
$FD^{2}\cdot AB+BF\cdot AF\cdot AB=BD^{2}\cdot AF+AD^{2}\cdot BF.$
In other words,
$FD^{2}\cdot AB+k^{2}(1-k^{2})=k^{2}(1-k^{2})+k^{2}AD^{2},$
i.e., $FD=kAD.$ Similarly, $DE=(1-k)AD.$ Adding up finalize the proof.
Acknowledgment
The above statement has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. The second proof is by Leo Giugiuc.
I placed proofs by Josué García Piscoya and Gobbalipur Jayanth on separate pages.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73606327
