Graphing Equations Is Useful

Graphing of equations would not give an exact solution (if any exists) but may provide an approximation and an insight into the properties of the equation that may help in finding a solution. Here is an example from the 1957 (XX) Moscow Mathematical Olympiad. The problem was offered to the 8th graders (equivalent at the time of the American sophomores):

Solve the system:

\( \displaystyle \begin{array}{3,2} \frac{2x_{1}^{2}}{1+x_{1}^{2}} &=x_{2}, \\ \frac{2x_{2}^{2}}{1+x_{2}^{2}} &=x_{3}, \\ \frac{2x_{3}^{2}}{1+x_{3}^{2}} &=x_{1}. \end{array} \)

Solution

Solve the system:

\( \displaystyle \begin{array}{3,2} \frac{2x_{1}^{2}}{1+x_{1}^{2}} &=x_{2}, \\ \frac{2x_{2}^{2}}{1+x_{2}^{2}} &=x_{3}, \\ \frac{2x_{3}^{2}}{1+x_{3}^{2}} &=x_{1}. \end{array} \)

It is rather obvious that the system represent iterations of function \(\displaystyle f(x)=\frac{2x^{2}}{1+x^{2}}\) and the question is to find a starting point \(x_{1}\) to which the iterations return after three applications of function \(f\). Let's graph \(y=f(x)\). (The straight line is the graph of \(y=x\).)

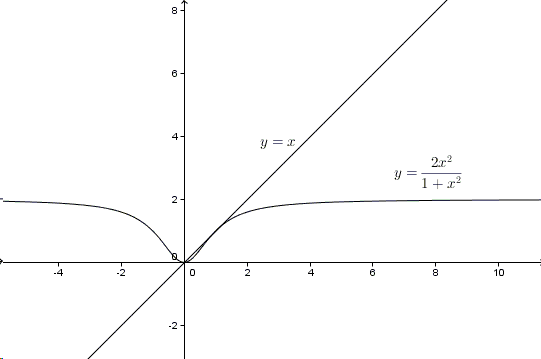
graph of the function y= 2x^2/(1+x^2)

The function is always positive such that the system may have only positive solutions. So here is a zoom into the first quadrant:

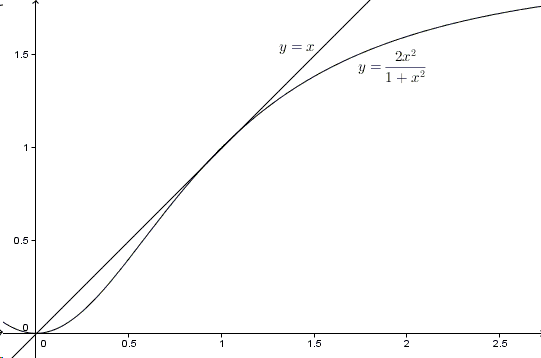
zoom into the graph of the function y= 2x^2/(1+x^2)

It appears that, except the points \((0,0)\), where the two graphs intersect, and \((1,1)\), where the graphs appear tangent), the graph of \(f\) is always below the line \(y=x\). As a consequence, for any non-negative \(x_{1}\),

\(x_{1}\ge f(x_{1}) = x_{2}\ge f(x_{2}) = x_{3}\ge f(x_{3}) = x_{1},\)

which implies that all three are equal. Thus the system does not have solutions other than \((0,0,0)\) and \((1,1,1)\).

The graph and the inequality \(f(x)\le x\) it suggests fill us with confidence that this is indeed so. But to make a rigorous proof, we still need to prove that inequality.

For the proof, I shall assume that \(x\gt 0\), for, \(f(0)=0\), and there is nothing else to prove.

Obviously, \((1-x)^{2} \ge 0\), i.e., \(2x \le 1+x^2\), which also can be written as \(\displaystyle\frac{2x}{1+x^{2}} \le 1\). Now, remembering that, by the assumption that \(x\gt 0\), we can multiply by \(x\) without disturbing the inequality:

\(\displaystyle f(x)=\frac{2x^{2}}{1+x^{2}}\le x.\)

This is exactly what we set out to prove. Thus the proof is complete.

To be fair, there is another proof - shorter than the above but that requires an extra insight.

Again, we shall assume that \(x\gt 0\). Under this assumption, let's replace the equations with their inverses:

\( \displaystyle \begin{array}{3,3} \left(\frac{1}{x_{1}}\right)^{2}+1=\frac{1+x_{1}^{2}}{x_{1}^{2}} &= 2\frac{1}{x_{2}}, \\ \left(\frac{1}{x_{2}}\right)^{2}+1=\frac{1+x_{2}^{2}}{x_{2}^{2}} &=2\frac{1}{x_{3}}, \\ \left(\frac{1}{x_{3}}\right)^{2}+1=\frac{1+x_{3}^{2}}{x_{3}^{2}} &=2\frac{1}{x_{1}}. \end{array} \)

Moving all the terms to the left and adding all three equations, we obtain

\( \displaystyle (1-\frac{1}{x_{1}})^{2}+(1-\frac{1}{x_{2}})^{2}+(1-\frac{1}{x_{3}})^{2}=0, \)

which implies that \(x_{1}=x_{2}=x_{3}=1\)

As the last remark, observe that the number of equations (and variables) is inconsequential. Both methods work equally well with any positive number of equations. This is not always the case.

Systems of Iterated Equations

71537043