Equation in Radicals as a System of Equations
What Might This Be About?
2August 2016, Created with GeoGebra
Problem
Here's a problem Imad Zak shared at his facebook page, with a credit to Adnan Y. I. Ajez. I believe the problem is old if not well known.
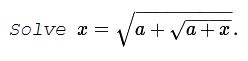
Solution 1
Introducing $y=\sqrt{a+x}\;$ we reduce the problem of solving an equation to that of solving a system of equations:
$y=\sqrt{a+x},\\ x=\sqrt{a+y}.$
It is hard to miss the point that the system may also result as an iteration on the function $f(x)=\sqrt{a+x}\;$ that formed a $2$-loop. Looking into the properties of the function $f(x),\;$ we may observe that all the iterations starting in the domain of the function converge when $a\gt -.25$ and none forms a $2$-loop
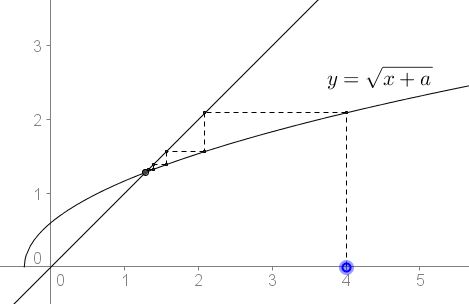
It thus follows that for the solution of the system, it this necessary that $y=x,\;$ implying the equation $x^2-x-a=0,\;$ with the only suitable solution being $\displaystyle x=\frac{1+\sqrt{1+4a}}{2}.$
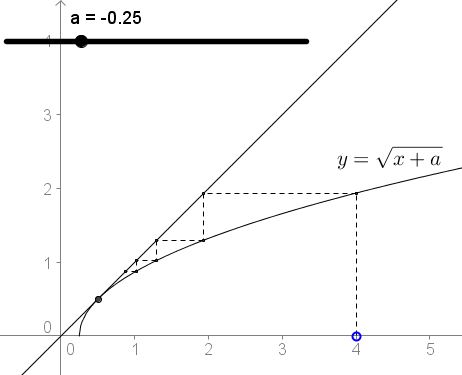
It is also clear what makes $a=-.25\;$ exceptional: for this $a,\;$ the graph of $f(x)=\sqrt{a+x}\;$ is tangent to the diagonal $y=x,\;$ instead of crossing it:
Solution 2
This solution is by Rachid Moussaoui.
Assume that the solution to the equation satisfies $x\gt\sqrt{a+x}.\;$ This would imply $a+x\gt a+\sqrt{a+x}.\;$ and, subsequently,
$x\gt\sqrt{a+x}\gt\sqrt{a+\sqrt{a+x}}=x.$
A contradiction. Similarly, assuming $x\lt\sqrt{a+x}\;$ also leads to a contradiction. It follows that necessarily $x=\sqrt{a+x},\;$ etc.
Solution 3
This solution is by Marco Antônio Manetta.
With $y=\sqrt{a+x},\;$ $x=\sqrt{a+y}\;$ and, subsequently $y^2=a+x\;$ and $x^2=a+y.\;$ Taking the difference gives $y^2-x^2=x-y,\;$ or $(x+y+1)(x-y)=0.\;$ $x\;$ and $y\;$ having to be non-negatve, $x+y+1=0\;$ is impossible. Therefore, $x=y,\;$ $x=\sqrt{a+x},\;$ and the proof ends as before.
Systems of Iterated Equations
- Iterations on Monotone Functions
- Graphing Equations Is Useful
- Graphing Equations Is Useful, II
- Graphing Equations Is Useful, III
- Graphing Equations Is Useful, IV
- Graphing Equations Is Useful, V
- Tangential Chaos
- Equation in Radicals as a System of Equations
- Two Conditions for a Triangle to Be Equilateral
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73572072
