Van Khea's Quickie
What Is This About?
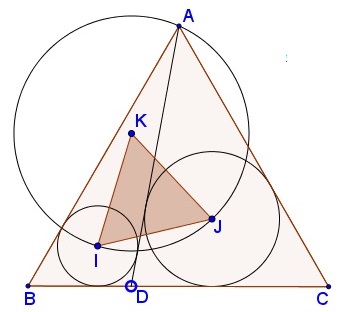
Problem

Solution
$AI\,$ is the bisector of $\angle BAD,\,$ $AJ\,$ is the bisector of $\angle CAD.\,$ Since $\angle BAC=60^{\circ},\,$ $\angle IAJ=30^{\circ}.\,$
Acknowledgment
The above problem was posted by Van Khea (Cambodia) at the Olimpiada pe Şcoală (The School Yard Olympiad) and commented with the above solution by Marian Dincă (Romania).
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73563028
