A Pedal Property in Equilateral Triangle
Miguel Ochoa Sanchez (Peru) has posted a problem and its solution (Proof 1) with a beautiful illustration I reproduce below.
Let point $P$ lie on the incircle of equilateral triangle $ABC.$ Let $D,E,F$ be the pedal points of $P$ on the sides of $\Delta ABC.$
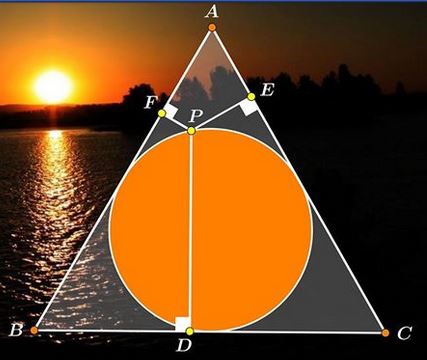
Prove that
$\displaystyle\frac{PD^{2}+PE^{2}+PF^{2}}{PD\cdot PE+PE\cdot PF+PF\cdot PD}=2.$
Proof 1
Elsewhere we derived a formula that related the areas of triangles $ABC$ and $DEF:$
$\displaystyle [\Delta EDF] = \frac{1}{4}(R^{2}-OP^{2})\cdot \frac{[\Delta ABC]}{R^{2}},$
where $O$ is the circumcenter of $\Delta ABC.$ For $P$ on the incircle (whose radius we denote $r$), the formula becomes
$\displaystyle [\Delta EDF] = \frac{1}{4}\bigg(1-\frac{r^{2}}{R^{2}}\bigg)\cdot [\Delta ABC].$
In equilateral triangle $R=2r$ so that for an equilateral $\Delta ABC,$ this simplifies to
$\displaystyle [\Delta EDF] = \frac{3}{16}[\Delta ABC].$
Assuming $AB=BC=AC=2,$ we get
(1)
$\displaystyle [\Delta EDF] = \frac{3\sqrt{3}}{16}.$
On the other hand, by Viviani's theorem, $PD+PE+PF=\sqrt{3},$ implying
(2)
$\begin{align} 3 &= (PD+PE+PF)^{2}\\ &= (PD^{2}+PE^{2}+PF^{2})+2(PD\cdot PE+PE\cdot PF+PF\cdot PD). \end{align}$
Also,
$\begin{align} [\Delta DEF] &= [\Delta DEP]+[\Delta EFP]+[\Delta FDP]\\ &=\frac{1}{2}(PD\cdot PE+PE\cdot PF+PF\cdot PD)\cdot\sin 120^{\circ}\\ &=\frac{\sqrt{3}}{4}(PD\cdot PE+PE\cdot PF+PF\cdot PD). \end{align}$
Combining this with (1) shows that $\displaystyle PD\cdot PE+PE\cdot PF+PF\cdot PD=\frac{3}{4}$. From (2) we then obtain $\displaystyle PD^{2}+PE^{2}+PF^{2}=\frac{3}{2}$ which implies the required ratio.
Proof 2
Leo Giugiuc has employed an entirely analytic approach by introducing coordinates: the incircle $x^{2}+y^{2}=1;$ $A=(0,2),$ $B=(-\sqrt{3},-1),$ $C=(\sqrt{3},-1);$ $P=(\cos t,\sin t),$ $t\in (\frac{\pi}{6},\frac{5\pi}{6});$ $AB:\,y-2=x\sqrt{3};$
$\begin{align}\displaystyle PD &= 1+\sin t,\\ PE &= \frac{2-\sqrt{3}\cos t-\sin t}{2}=\frac{2-2\sin (t+\frac{\pi}{3})}{2},\\ PF &= \frac{2+\sqrt{3}\cos t-\sin t}{2}=\frac{2+2\sin (t+\frac{2\pi}{3})}{2}. \end{align}$
From here,
$\begin{align}\displaystyle \sqrt{PD} &= \sin\frac{t}{2}+\cos\frac{t}{2},\\ \sqrt{PE} &= \sin(\frac{t}{2}+\frac{\pi}{6})-\cos(\frac{t}{2}+\frac{\pi}{6}),\\ \sqrt{PF} &= \sin(\frac{t}{2}+\frac{\pi}{3})+\cos(\frac{t}{2}+\frac{\pi}{3}).\\ \end{align}$
With a little more effort one gets $\sqrt{PD}=\sqrt{PE}+\sqrt{PF}.$ Note that this identity is a special case of a more general one
$\displaystyle\sqrt{PD}\cos\frac{A}{2}=\sqrt{PE}\cos\frac{B}{2}+\sqrt{PF}\cos\frac{C}{2}$
where, for an equilateral triangle $A=B=C=\frac{\pi}{3}.$ Given that, the required identity follows from
$\displaystyle 2(xy+yz+zx)-(x^{2}+y^{2}+z^{2})=(\sqrt{x}+\sqrt{y}+\sqrt{z})\prod_{cycl}(-\sqrt{x}+\sqrt{y}+\sqrt{z})=0,$
the product is of three factors each of the form $(\pm\sqrt{x}\pm\sqrt{y}\pm\sqrt{z}),$ with only one minus sign in each.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573065
