Converse Construction in Pompeiu's Theorem

Form an equilateral triangle $BCD,\,$ with $BC\,$ separating $A\,$ and $D,\,$ and another one $ADE,\,$ with $B\,$ in its interior.

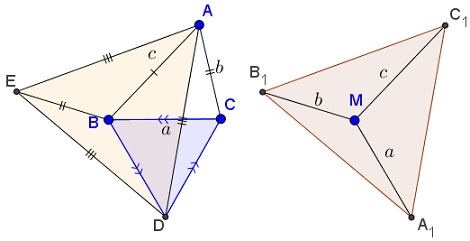
We'll prove that $\Delta ADE\,$ is the sought equilateral triangle, with $B\,$ playing the role of $M.\,$

Indeed, by the construction, $BD=BC=a,\,$ $BA=c.\,$ It remains to verify that $BE=b.\,$ Observe that the counterclockwise rotation around $D\,$ through $60^{\circ}\,$ moves $C\,$ to $B,\,$ $A\,$ to $E\,$ and, therefore, $AC\,$ to $BE,\,$ proving that $BE=AC=b.$

In passing, $\angle C_1MA_1=\angle ABD =\angle ABC+60^{\circ}.\,$ It follows from the diagram below that $\angle B_1MC_1=\angle EBA=\angle BAC+60^{\circ}:$

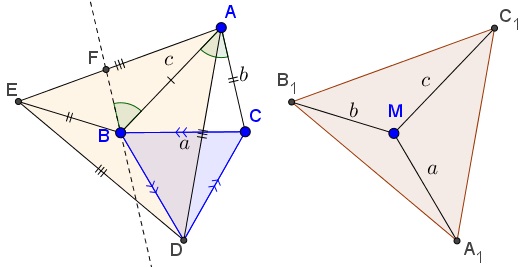
Similarly, $\angle A_1MB_1=\angle DBE=\angle ACB+60^{\circ}.$

Consider Napoleon's triangles $ABC',\,$ $BCA',\,$ $CAB'.\,$ The Fermat-Torricelli point $F\,$ is the intersection of $AA',\,$ $BB',\,$ $CC'.\,$ It is also a common point of the three circumcircles $(ABC'),\,$ $(BCA'),\,$ $(CAB')\,$ whose centers we denote $C_0,\,$ $A_0,\,$ and $B_0,\,$ respectively.

From the concurrency of the circumcenters at point $F,\,$ $A_0F=A_0A'=\frac{\sqrt{3}}{3}a,\,$ $B_0F=B_0B'=\frac{\sqrt{3}}{3}b,\,$ $C_0F=C_0C'=\frac{\sqrt{3}}{3}c.\,$ By Napoleon's theorem, $\Delta A_0B_0C_0\,$ is equilateral. All that remains is to expand the diagram by a factor $\sqrt{3}.$

We choose an arbitrary point $M\,$ and construct points $A_1,B_1,C_1\,$ such that $A_1M=a,\,$ $B_1M=b\,$ $C_1M=c\,$ and $\angle B_1MC_1=\angle A+\displaystyle\frac{\pi}{3},\,$ $\angle C_1MA_1=\angle B+\displaystyle\frac{\pi}{3},\,$ $\angle A_1MB_1=\angle C+\displaystyle\frac{\pi}{3}.\,$ It is easily verifies that $\angle B_1MC_1+\angle C_1MA_1+\angle A_1MB_1=2\pi.$

Now compute the side length of $\Delta A_1B_1C_1:$

$\displaystyle\begin{align} |B_1C_1|^2 &= b^2+c^2-2bc\cos\left(\angle A+\frac{\pi}{3}\right)\\ &=b^2+c^2-2bc\left (\cos\angle A\cdot\frac{1}{2}-\sin\angle A\cdot\frac{\sqrt{3}}{2}\right)\\ &=b^2+c^2+\frac{a^2-b^2-c^2}{2}+\sqrt{3}bc\sin\angle A\\ &=\frac{a^2+b^2+c^2+\sqrt{3}[\Delta ABC]}{2}, \end{align}$

where $[\Delta ABC]=\frac{1}{2}bc\sin\angle A\,$ is the area of $\Delta ABC.\,$ Since the expression is symmetric in $a,b,c\,$ it is clear that $B_1C_1=C_1A_1=A_1B_1.\,$

With Heron's formula, the side length $\ell\,$ of $\Delta A_1B_1C_1\,$ can be expressed strictly in terms of the side lengths $a,b,c:$

$\displaystyle \ell^2=\frac{a^2+b^2+c^2+\sqrt{3(2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4)}}{2}.$

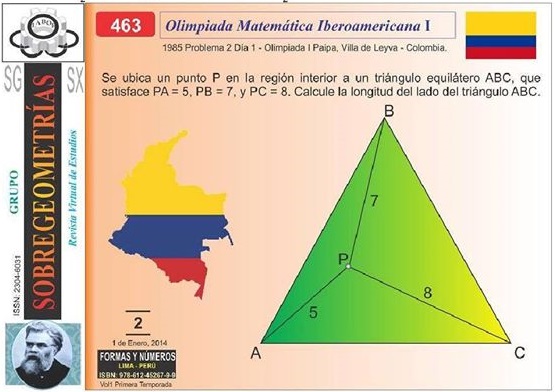
The problem is solved by picking $a=5,\,$ $b=7,\,$ and $c=8:$

$\displaystyle\ell^2=\frac{5^2+7^2+8^2+\sqrt{3(25^27^2+27^28^2+28^25^2-5^4-7^4-8^4)}}{2}=129.$

The problem and Solution have been shared on facebook by Marian Dinca. He used his soliton to answer the olympiad question above. As he observed, the problem is, in a sense, the converse of Pompeiu's Theorem. Construction 2 is by Chris van Tienhoven.