Equilateral Triangle in Equilateral Triangle

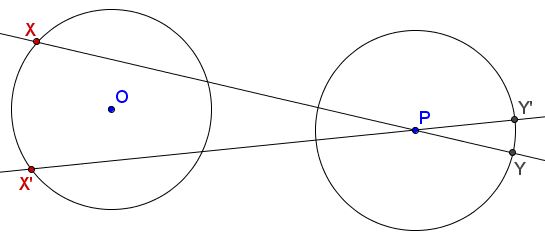
To start with, consider two circles $(O)$ and $(P)$ of the same radius. Let $X$ be an arbitrary point on $(O).$ Join $X$ to $P$ and let $Y$ be the father intersection of $XP$ with $(P).$ Consider mapping $T:\space (O)\rightarrow (P),$ defined with $X\mapsto Y.$ I claim that $T$ is a contraction mapping.

To make that more precise, define metrics $d_O$ and $d_P$ on $(O)$ and $(P),$ respectively as the angular distances between their points, e.g., in the diagram below, $d_{O}(X,X')=\angle XOX'.$ (To be even more precise we may restrict $T$ to the portion of $(O)$ that consists of more distant points of intersection with $(O)$ of lines through $(P).)$

Then, with $Z$ and $Z'$ as shown,

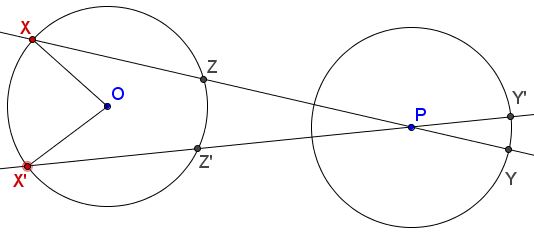
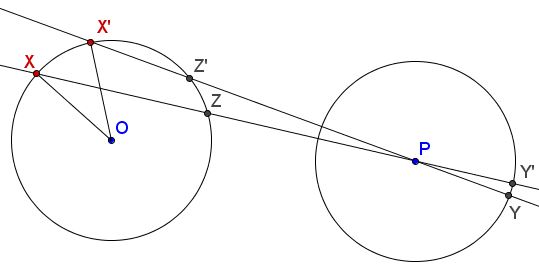
$\begin{align} d_{P}(Y,Y')&=\angle YPY'=\angle XPX'=\frac{1}{2}(\overparen{\rm XX'}-\overparen{\rm ZZ'})\\ &\lt \frac{1}{2}\overparen{\rm XX'}=\frac{1}{2}\angle XOX'\\ &=\frac{1}{2}d_{O}(X,X'). \end{align}$

Now, back to the problem at hand.

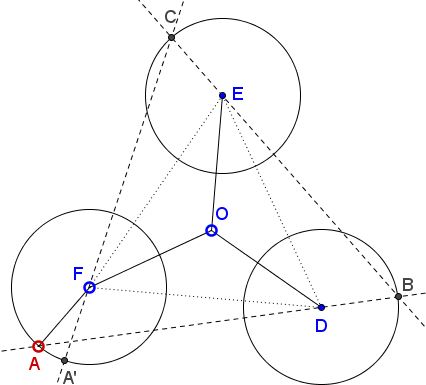
Pick point $A\in (F),$ map it on $B\in (D),$ and from here to $C\in(E),$ and to $A'\in(F).$ All three auxiliary mappings are contractions with the same coefficient $\frac{1}{2}$ such that the mapping of $(O)$ to itself, defined by $A\mapsto A',$ is a contraction with the coefficient $\frac{1}{8}\lt 1.$ According to the Contraction Mapping Theorem there exists a unique fixed point, say, $A_0.$

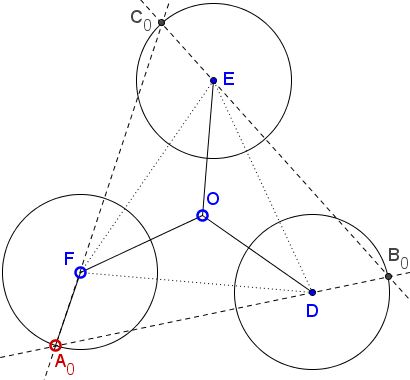
This defines $B_0$ and $C_0$ such that $\Delta A_{0}B_{0}C_{0}$ is equilateral for, otherwise, a rotation by $120^{\circ}$ around $O$ would place $B_0$ on $(F)$ different from $A_0$ and make it another fixed point on $(F).$ So it follows that $A_{0},B_{0},C_{0}$ are obtained from each other with a rotation through $120^{\circ}$ around $O,$ making $\Delta A_{0}B_{0}C_{0}$ equilateral indeed.

Note 1: To apply the Contraction Mapping Theorem we need to make sure that the metric $d_O$ makes $(O)$ a complete metric space. This is left as an exercise.

Note 2: The polygon in the statement need not be a triangle. A similar construction starting with an $n\mbox{-gon},$ $n\gt 3,$ would lead to another regular $n\mbox{-gon}.$

The problem has been posted by Omer Simhi (Haifa, Israel) at the CutTheKnotMath facebook page.