Symmedian and the Tangents
What is this about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander BogomolnyA symmedian through one of the vertices of a triangle passes through the point of intersection of the tangents to the circumcircle at the other two vertices.
| Buy this applet What if applet does not run? |
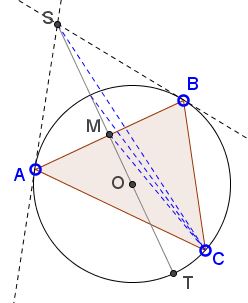
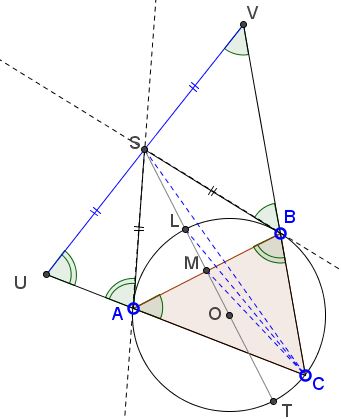
The proof is based on a known fact: the locus of the midpoints of the antiparallels to a side of a triangle is the summedian through the opposite vertex. Draw an antiparallel through S - the point of intersection of the two tangents to the circumcircle of the triangle ABC at A and B. Let it meet the extended sides AC and BC at U and V, respectively. Then the triangles USA and VSB are isosceles, so that
|
SU = SA and SV = SB. |
In addition,
| SA = SB, |
as two tangents from a point to a circle. We conclude that S is the midpoint of UV. Therefore, S belongs to the locus of all such midpoints. Since the locus is the symmedian - a straight line - through the vertex C, CS is bound to be that symmedian.
References
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49551980 |
