Symmedian and 2 Antiparallels
What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applets illustrates the following statement:

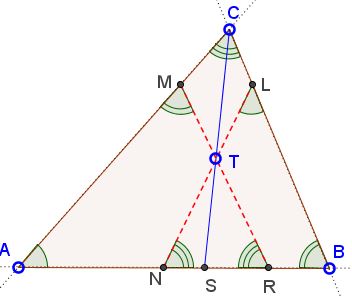
Let CS be the symmedian and MR and LN the two antiparallels in question that meet in point T on CS. Triangle RTN having equal base angles at R and N is isosceles. Therefore,

(1)

TN = TR.

Draw the third antiparallel UV through T.

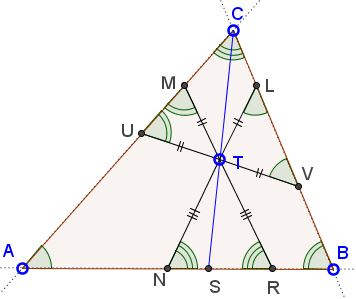
Similarly to the above, we have

TL = TV and
TM = TU.

However, as we know,

TU = TV.

Therefore

MR	= TM + TR
	= TL + TN
	= LN.

Note that we actually got a little more than claimed: the corresponding pieces of the equal antiparallels cut off by the symmedian are also equal.

By transitivity, the three antiparallels through the symmedian point all have equal lengths.

Symmedian

1. All about Symmedians
2. Symmedian and Antiparallel
3. Symmedian and 2 Antiparallels
4. Symmedian in a Right Triangle
5. Nobbs' Points and Gergonne Line
6. Three Tangents Theorem
7. A Tangent in Concurrency
8. Symmedian and the Tangents
9. Ceva's Theorem
10. Bride's Chair
11. Star of David
12. Concyclic Circumcenters: A Dynamic View
13. Concyclic Circumcenters: A Sequel
14. Steiner's Ratio Theorem
15. Symmedian via Squares and a Circle
16. Symmedian via Parallel Transversal and Two Circles
17. Symmedian and the Simson
18. Characterization of the Symmedian Point with Medians and Orthic Triangle
19. A Special Triangle with a Line Through the Lemoine Point

Related material Read more...
	What Is Antiparallel?
	Antiparallel via Three Reflections
	Symmedian and Antiparallel
	Tucker Circles
	Circle through the Incenter And Antiparallels
	Batman's Problem
	Antiparallel and Circumradius

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny