The Star of David
A. Bogomolny
Let's start with a nice configuration I have referred to on a couple of occasions. A billiard ball has been kicked at a 60° angle to a side of a billiard table in the form of an equilateral triangle. After bouncing twice from each side, the ball eventually returns to its starting point. The distance travelled does not depend on the latter and remains constant, except for one case. If the ball starts in the middle of a side, then it returns to that point only after a three legged journey, which is only half as long as for other starting points. If we consider the length of the trajectory between two traversals of the starting point as a function of that point, we get an example of a naturally discontinuous function.
From a geometric viewpoint, we are given a hexagon inscribed into an equilateral triangle. What can be said about that hexagon? By construction, at vertices, its sides are equally inclined to the sides of the triangle. This reminds us of the mirror property enjoyed by the orthic triangle. May we then generalize the original configuration to an arbitrary triangle? Yes, this is possible if we draw lines parallel to the sides of the orthic triangle.
This procedure generates a closed curve -- a hexagon or a triangle -- whose length is a discontinuous function of its position as defined by, say, any of its vertices. (Observation: the sides of the hexagon intersect on the altitudes of the triangle. When three sides are concurrent, they intersect at the orthocenter of the triangle.)
We are not done yet. The original configuration permits one other Description. For example, we may notice that the sides of the hexagon are parallel to the sides of the given equilateral triangle. This construction can also be generalized:Drawing lines parallel to the sides of an arbitrary triangle we also get a closed curve, a hexagon to be exact, except for the case when we start at a mid point of a side, in which case we obtain the medial triangle. And the length of the curve is again a discontinuous function of the starting point. (Observation: the sides of the hexagon intersect on the medians of the triangle. When three sides are concurrent, they intersect at the centroid of the triangle.)
Well, starting with an absurd billiard table we obtained two apparently unrelated configurations. In one, the inscribed hexagon has its sides parallel to the sides of the orthic triangle. In the other case, the sides of the hexagon are parallel to the sides of the given triangle. However, there is a little more to it. The orthic triangle has an interesting property. The medial triangle cuts from the given one three triangles similar to the given triangle. This is obvious as the triangles have parallel sides. Interestingly, the orthic triangle has exactly same property. It cuts off three triangles similar to the given one.
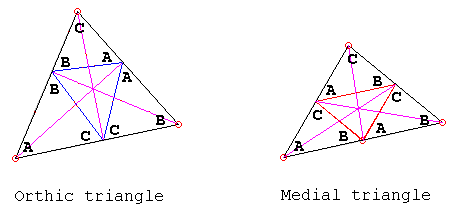
The difference between the two cases is that now, the angles are in the reversed order. The sides of the medial triangle are parallel to the sides of the base triangle. The sides of the orthic triangle are said to be antiparallel to the corresponding sides of the given triangle.
Let's summarize what we got so far. If in a given triangle starting with a given point we draw parallels or antiparallels to successive sides, in both cases we obtain a closed curve -- a hexagon, which sometimes degenerates into a triangle. Well, the fun does not stop here. It so happens that, in a sense, it is possible to combine the two constructions into one. Namely, let's draw a parallel followed by an antiparallel followed by a parallel, and so on.
Far as getting a closed curve is concerned, we do get one -- again a hexagon. We lose some, we gain some. The hexagon does not appear to degenerate into a triangle. But it does have some interesting properties. First of all, the hexagon is cyclic: its vertices always lie on a circle. The circles are known as the Tucker circles. The hexagons also bear Tucker's name.
Two of the hexagons have three concurrent sides. In one case, the concurrent sides are parallel to the sides of the given triangle, in the other they are antiparallel. In both cases, the circles bear the name of Lemoine: the first and the second Lemoine circles. The case of the second Lemoine circle is somewhat simpler. The antiparallel sides intersect at its center and therefore serve as its diameters. The point of intersection -- the center of the second Lemoine circle -- is known as the Lemoine point. The hexagon is known as the Lemoine hexagon; its sides that pass through the Lemoine point are the Lemoine antiparallels.
The fact that, in this case, three sides serve as diameters of the Lemoine circle has a corollary. Split the vertices of the hexagon into two groups of three, say, odd and even numbered vertices. What we get is two triangles with sides perpendicular to the sides of the given triangle, but differently oriented. Moreover, vertices of the two triangles are pairwise connected by lines (the sides of the hexagon) parallel to the given triangle. The triangles are therefore equal. Being perpendicular to a side means being parallel to the corresponding altitude. Now, altitudes constitute a particular case of concurrent Cevians. Is there a generalization? Yes, indeed there is.
Take a point in the plane of a triangle and the Cevians through that point. There exist two triangles inscribed into the given one with sides parallel to the Cevians. When the Cevians are altitudes, the triangles combine into a Tucker hexagon inscribed into the second Lemoine circle. In the general case, the hexagon is no longer cyclic, but the triangles are still equal and centrally symmetric.
Hidefumi Katsuura from San Jose State University invented an iterative process that leads to that configuration. Start with a point (click anywhere in the applet) and draw a perpendicular to a side of a given triangle. From there drop a perpendicular to another side and so on. Putting it a little differently, the process requires us to draw lines parallel to the altitudes of a given triangle. This can be accomplished in two ways, depending on the ordering of the altitudes. Both processes converge, each to a triangle. And not surprisingly, these are exactly the triangles we just met above. The story was described by D. Gale in The Mathematical Intelligencer and subsequently in his book.
H. Katsuura has noted that the resulting configuration of the two limit triangles resembles the Star of David, albeit a distorted star when the given triangle is not equilateral.
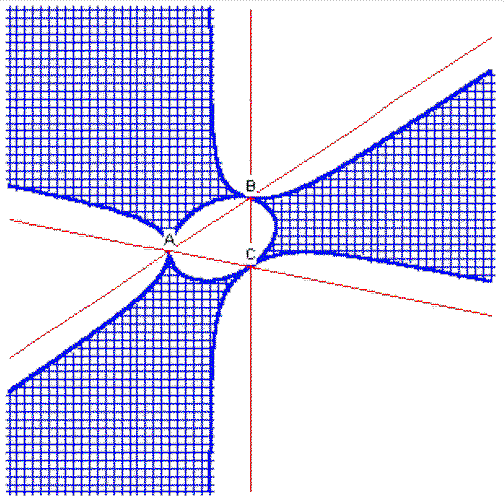
Of course there is an interesting generalization. Two iterative processes may be run for any three concurrent Cevians. However depending on the point of concurrence, the iterations may or may not converge.
Jean-Pierre Ehrmann -- a French member of the Hyacinthos discussion group -- produced the following diagram where the region of divergence is marked in blue.
Related to the above are the following two exercises.
This one is relatively easy. From the base vertices, draw two arbitrary lines to the sides opposite the vertices. From there draw two additional lines parallel to the previous ones. The two points of intersection of the latter with the sides of the triangle lie on a line parallel to the base.
The second one is difficult. Let's make it a math droodle. What is it? The combination of the two proves that, in the presence of convergence, the limit triangles are always equal.
References
- D. Gale, Tracking The Automatic Ant, Springer, 1998
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
- H. Katsuura, Star of David, SJSU, unpublished manuscript
- Why Not Geometry?
- A critical look at a newspaper article
- A nice piece of geometry
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
- Steiner's Ratio Theorem
- Symmedian via Squares and a Circle
- Symmedian via Parallel Transversal and Two Circles
- Symmedian and the Simson
- Characterization of the Symmedian Point with Medians and Orthic Triangle
- A Special Triangle with a Line Through the Lemoine Point
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573963
