Symmedian in a Right Triangle
What is this about?
A Mathematical Droodle
Explanation
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
The applet suggests a simple fact that, in a right triangle, the symmedian to the hypotenuse coincides with the altitude from the right angle.
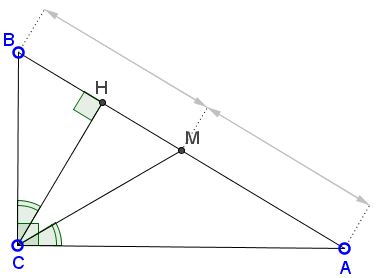
A symmedian is the isogonal conjugate of a median from the same vertex. Thus, for example, in right triangle ABC, with the right angle at C, if CM is the median and CH is the symmedian through C, then angles ACM and BCH are equal. But in a right triangle, the median through the right angle equals half the hypotenuse, so that triangle AMC is isosceles. Its base angles MCA and MAC are equal. We thus have
| |
∠CAB = ∠BCH,
∠CAB + ∠ABC = 90°, and
∠ABC = ∠HBC.
|
Therefore
It thus follows that angle CHB is right, as asserted.
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
|
