Symmedian via Squares and a Circle

Form squares $ABGF\;$ and $ACDE\;$ in the exterior of $\Delta ABC.\;$ Let $O\;$ be the center of circle $(AEF),\;$ as shown

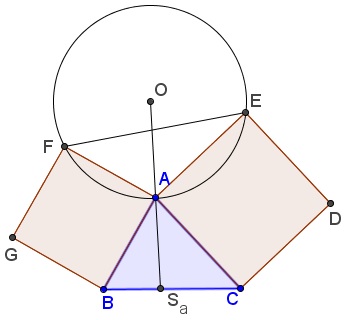
Squares and a circle lead to a symmedian, problem

Then that the line $OA\;$ is the symmedian in $\Delta ABC\;$ through vertex $A.$

Proof 1

The distance from $O\;$ to $AB\;$ equals $\displaystyle d(O,AB)=OJ=\frac{1}{2}AF=\frac{1}{2}AB:$

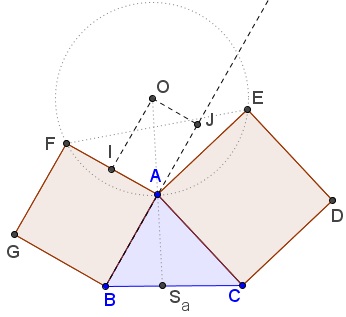
Squares and a circle lead to a symmedian, solution 1

Similarly the distance $\displaystyle d(O,AC)=\frac{1}{2}AC.\;$ It follows that $\displaystyle \frac{d(O,AB)}{d(O,AC)}=\frac{AB}{AC}\;$ which is one of the characteristic properties of the symmedian.

Proof 2

The configuration of two squares on the sides of a triangle is a part of the well known Bride's Chair; $\Delta AEF\;$ is a flank triangle of $\Delta ABC.\;$ The altitude through $A\;$ in the former is the median through $A\;$ in the latter:

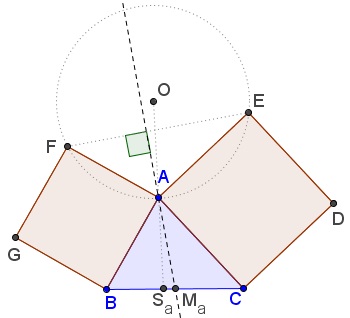
Squares and a circle lead to a symmedian, solution 2

It is also true that angles $BAC\;$ and $EAF\;$ share the angle bisector. On the other hand, in $\Delta AEF\;$ the orthocenter and the circumcenter are isogonal conjugate, implying that the altitude through $A\;$ is isogonal to $AO.\;$ Thus, in $\Delta ABC,\;$ the line $AO\;$ is isogonal to the median $AM_a\;$ and, therefore, is the symmedian through $A.$

References

Sammy Luo and Cosmin Pohoata, Let's Talk About Symmedians!, Mathematical Reflections 4 (2013), 1-11

Symmedian

73361198