Seven Problems in Equilateral Triangle
Solution to Problem 1

Given an equilateral triangle $ABC$ with the base extended to twice its length: $AB'=AB.$ $B'E$ and $B'F$ are tangent to the circumcircle $(ABC).$

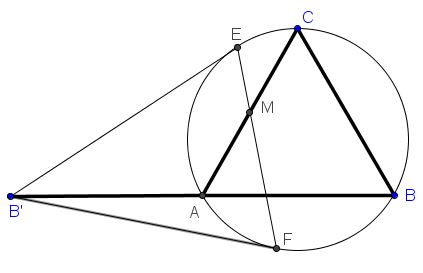
Problem 1 in equilateral triangle with one side extanded

Prove that $EF$ passes through the midpoint $M$ of $AC.$

Solution

Join $B'$ to $C.$ By the construction, $AB'=AC$ so that $\Delta B'AC$ is isosceles, with $\angle B'AC=120^{\circ},$ implying $\angle B'CA=30^{\circ} = \angle OBA,$ where $O$ is the center/circumcenter of $\Delta ABC.$ If $D$ is opposite $B$ on the circumcircle (i.e., if $BD$ is a diameter), $\angle DCA=\angle DBA=\angle OBA$ from which $\angle DCA = \angle B'CA$ and, therefore,$D$ is the intersection of $B'C$ and $(ABC).$

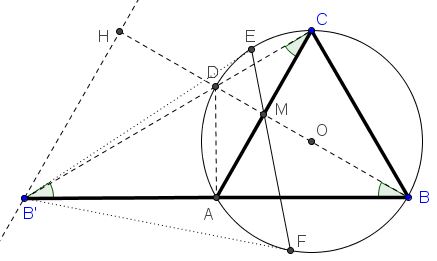
Problem 1 in equilateral triangle with one side extanded, solution

Let $R$ be the radius of $(ABC).$ We have $OM=MD=R/2.$ The polar of point $M$ relative to $(ABC)$ is perpendicular to $OM$ and passes through point $H$ that satisfies $OH\cdot OM=R^2.$ It follows that $OH=2R.$ Since $OM=R/2,$ we also have $HM=3R/2=BM,$ making triangles $BHB'$ and $BMA$ similar (same angle at $B$ and proportional enclosing sides.) Thus $B'H\perp BH$ and $B'H$ is the polar of point $M.$ By La Hire's theorem, the polar of $B'$ passes through $M$ but this is exactly $EF,$ and the proof is complete.

Acknowledgment

The proof only a slight modification of the one suggested by Machó Bónis at the CutTheKnotMath facebook page.

Poles and Polars

71868313

Seven Problems in Equilateral Triangle Solution to Problem 1

Solution

Acknowledgment

Poles and Polars

Seven Problems in Equilateral Triangle
Solution to Problem 1