Symmedian via Parallel Transversal and Two Circles

What Is This About?

Problem

Let $MN\;$ be a transversal parallel to the side $BC\;$ of $\Delta ABC,\;$ with $M\;$ on $AB\;$ and $N\;$ $AC.\;$ The lines $BN\;$ and $CM\;$ meet at point $P.\;$ The circumcircles of triangles $BMP\;$ and $CNP\;$ meet at two distinct points $P\;$ and $Q.\;$

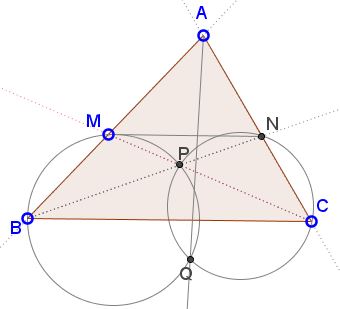
Symmedian via Parallel Transversal and Two Circles, problem

Prove that the line $AQ\;$ is the $A\text{-symmedian}\;$ of $\Delta ABC.$

Proof

Consider triangles $BQM\;$ and $NQC:$

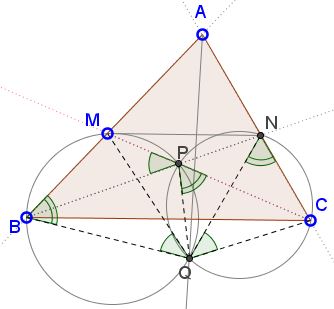
Symmedian via Parallel Transversal and Two Circles, solution

We start with angle chasing:

(1)

$\angle BQM=\angle BPM=\angle CPN=\angle CQN.$

Also,

(2)

$\angle MBQ=180^{\circ}-\angle MPQ=\angle CPQ=\angle CNQ.$

Form (1) and (2), triangles $BQM\;$ and $NQC\;$ are similar and their respective elements are proportional. It follows that

$\displaystyle\frac{dist(Q,AB)}{dist(Q,AC)}=\frac{dist(Q,BM)}{dist(Q,CN)}=\frac{BM}{CN}=\frac{AB}{AC},$

implying that $AQ\;$ is indeed the symmedian in $\Delta ABC\;$ through vertex $A.$

References

  1. Sammy Luo and Cosmin Pohoata, Let's Talk About Symmedians!, Mathematical Reflections 4 (2013), 1-11

 

Symmedian

  1. All about Symmedians
  2. Symmedian and Antiparallel
  3. Symmedian and 2 Antiparallels
  4. Symmedian in a Right Triangle
  5. Nobbs' Points and Gergonne Line
  6. Three Tangents Theorem
  7. A Tangent in Concurrency
  8. Symmedian and the Tangents
  9. Ceva's Theorem
  10. Bride's Chair
  11. Star of David
  12. Concyclic Circumcenters: A Dynamic View
  13. Concyclic Circumcenters: A Sequel
  14. Steiner's Ratio Theorem
  15. Symmedian via Squares and a Circle
  16. Symmedian via Parallel Transversal and Two Circles
  17. Symmedian and the Simson
  18. Characterization of the Symmedian Point with Medians and Orthic Triangle
  19. A Special Triangle with a Line Through the Lemoine Point

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny

73362574