Symmedian and the Simson
What is this about? A Mathematical Droodle
Problem
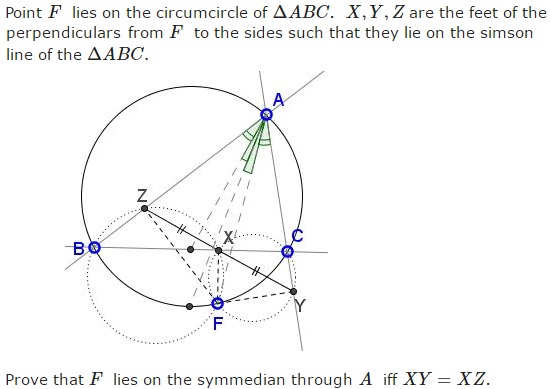
Proof 1
We first assume that $F\;$ lies on the symmedian from $A\;$ and shall repeatedly apply the Law of Sines.
In $\Delta FXZ,\;$ $\displaystyle\frac{XZ}{FX}=\frac{\sin\angle XFZ}{\sin\angle FZX}\;$ in $\Delta XYF,\;$ $\displaystyle\frac{XY}{FX}=\frac{\sin\angle XFY}{\sin\angle FYX}.\;$ Eliminating $FX$ gives
(1)
$\displaystyle\frac{XZ}{XY}=\frac{\sin\angle XFZ}{\sin\angle XFY}\cdot\frac{\sin\angle FYX}{\sin\angle FZX}.$

In $\Delta FYZ,\;$ $\displaystyle \frac{\sin\angle FYX}{\sin\angle FZX}=\frac{\sin\angle FYZ}{\sin\angle FZY}=\frac{FZ}{FY}.\;$ Since $F\;$ lies on the symmedian, it follows that $\displaystyle \frac{FZ}{FY}=\frac{AB}{AC}.$
On the other hand, quadrilateral $BFXZ\;$ is cyclic so that $\angle XFZ=\angle XBZ =\angle ABC.\;$ Similarly, $\angle XFY=\angle ACB.\;$ In $\Delta ABC,\;$ $\displaystyle\frac{\sin\angle XFZ}{\sin\angle XFY}=\frac{\sin\angle ABC}{\sin\angle ACB}=\frac{AC}{AB}.$
Substituting our finds into (1) shows that
$\displaystyle\frac{XZ}{XY}=\frac{AB}{AC}\cdot\frac{AC}{AB}=1.$
implying $XY=XZ.$
Conversely, assume $XY=XZ.$ Then (1) becomes,
$\displaystyle 1=\frac{\sin\angle XFZ}{\sin\angle XFY}\cdot\frac{\sin\angle FYX}{\sin\angle FZX}=\frac{AC}{AB}\cdot\frac{FZ}{FY},$
implying $\displaystyle\frac{FY}{FZ}=\frac{AC}{AB},\;$ which is a characteristic property of points on the symmedian.
Proof 2
Let $E\;$ be the point on the circle where $EF\parallel BC,\;$ $F'\;$ be the point of intersection of $AE\;$ and $FX.\;$ We make the following observations:

It immediately follows that $AF\;$ and $AE\;$ isogonal conjugates of triangles $BAC\;$ and $ZAY\;$ too. Since $AF\;$ is diameter of circumcircle $ZAY\;$ (quadrilateral $AZFY\;$ is cyclic) it follows that $AE\;$ perpendicular to the Simson line $XYZ,\;$ i.e., $F'\;$ is the intersection of the altitudes of $\Delta ZAY.$
In $\Delta ZAY,\;$ point $X\;$ on side $ZY\;$ bisects $FF'\;$ if and only if $F'\;$ is the orthocenter of that triangle, in other words, $FX=F'X\;$ is equivalent to $ZX=XY\;$ $(FZFY\;$ must be a parallelogram.)
If we look now at right triangle $EFF'\;$ we'll see that $FX=F'X\;$ iff $M_a\;$ is on the hypotenuse $EF'\;$ as the circumcenter of that triangles $(AE\;$ is a median).
Thus we arrive at the following conclusions:
Line $AE\;$ is perpendicular to the simson line of point $F\;$ iff $AE,\;$ $AF\;$ are isogonal conjugates.
$ZX=XY\;$ is equivalent to $AM_a\;$ being perpendicular to $XYZ.$
Proof 3
The condition $ZX=XY\;$ can be rewritten as: $BF\cdot\sin (B) = CF\cdot\sin(C)\;$ which is equivalent to
$\displaystyle\frac{AC}{BC}=\frac{\sin(B)}{\sin(C)} = \frac{\sin(CAF)}{\sin(BAF)}=\frac{FY}{FZ}.$
But this is one of the characteristic properties of the symmedian.
Acknowledgment
- The statement and Proof 2 are due to Vladimir Nikolin who posted both at the CutTheKnotMath facebook page. Vladimir also posted a proof (Proof 3) from the artofproblemsolving site.
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
- Steiner's Ratio Theorem
- Symmedian via Squares and a Circle
- Symmedian via Parallel Transversal and Two Circles
- Symmedian and the Simson
- Characterization of the Symmedian Point with Medians and Orthic Triangle
- A Special Triangle with a Line Through the Lemoine Point
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73562834
