Poles, Polars and Orthogonal Circles

Given circles \(A(BD)\) and point \(C(BD)\), with centers at \(A\) and \(C\), meeting in points \(B\) and \(D\), let \(E\) be any point on \(BD\). Draw tangents \(EF\), \(EG\) from \(E\) to \(A(BD).\)

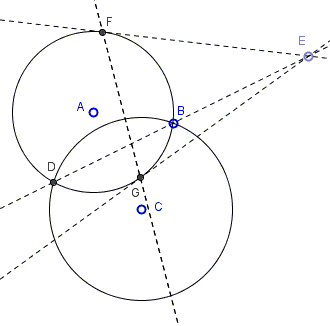
Two circles, tangents, and a chord in one circle through the center of the other - problem

Then \(FG\) passes through \(C\) if and only if the two circles are orthogonal.

Solution

Below is an applet that is supposed to illustrate the assertion:

When you drag points or lines in the applet, the objects leave a trace. To remove the traces press Reset. If you do, drag point \(E\) along \(BD.\) You will be able to observe that the lines \(FG\) all pass through a fixed point. This point is the pole of chord \(BD\) in \(A(BD).\) You may surmise that that pole coincides with \(C\) only if the two circles are orthogonal.

Two circles, tangents, and a chord in one circle through the center of the other - problem

Then \(FG\) passes through \(C\) if and only if the two circles are orthogonal.

The polar of a point outside a circle with respect to that circle is defined by the two points of tangency of the tangents from the point to the circle.

Point \(E\), therefore, is known to be the polar of chord \(FG.\) Since \(E\) is chosen on \(BD,\) the pole of the latter, by La Hire's theorem, lies necessarily on the polar of the former.

Two circles, tangents, and a chord in one circle through the center of the other - illustration

Let's \(P\) stands for the polar of \(BD.\) Then \(PF\) is tangent to \(A(BD)\) only if \(PF\perp AF,\) implying that \(P\) is the center of circle \(C(BD),\) or that the two circles are orthogonal.

71869167