Archimedes' Twin Circles and a Brother: What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

One of the properties of the arbelos noticed and proved by Archimedes in his Book of Lemmas is that the two small circles inscribed into two pieces of the arbelos cut off by the line perpendicular to the base through the common point of the two small semicircles are equal. The circles have been known as Archimedes' Twin Circles. More than 2200 years after Archimedes, L. Bankoff (1974) has found another circle equal to the twins.

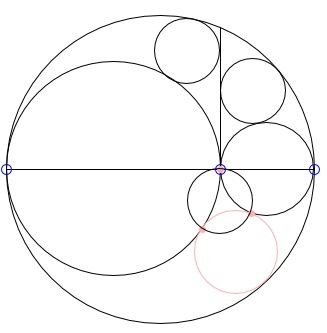
The best way to see the circle is to reflect the arbelos in the common base of its constituent semicircles. Proposition 6 of the Book of Lemmas deals with the circle tangent to all three semicircles. The two points of tangency with the small semicircles together with the point C in the applet form a triangle whose circumcenter has the same radius as Archimedes' twins!

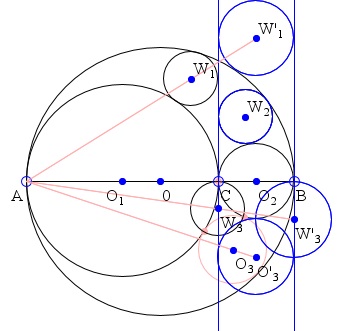
For definiteness' sake, let the semicircles have centers O, O₁, O₂. Following Bankoff's convention, a circle will be denoted by the same letter as its center enclosed in a couple of parentheses. Thus, e.g. the big semicircle is the top part of (O). The twin circles are, say, (W₁) and (W₂), and the circle due to Proposition 6 is (O₃). The circle in question is (W₃).

To prove this result we shall use the inversion with center A and the power equal to AC·AB.

The inversion swaps B and C, and further

Denote the radii of the circles (O), (O₁), (O₂), (O₃),(W₁), (W₂), (W₃), (O'₁), (O'₃), (W'₁), (W'₃) as R, R₁, R₂, R₃, p₁ = p₂ = p, p₃, R'₁, R'₃, p', p'₃, respectively. Note that p' = R₂.

We have the following:

1. Since A is the external center of similitude of (W₁) and (W'₁),

   p/p' = (2R1 - p)/(2R1 + R2),

   from which

   p = R1·R2/R = R1·R2/(R1 + R2).

   
   

2. In the triangles ACW₃ and ABW'₃

   p3/p'3 = AC/AB = R1/R

   and it follows that

   p3 = R1·p'3/R = R1·R2/R.

   
   

Note that in terms of R₁ and R₂, Archimedes' formula becomes

Remark

As an aside, the foregoing reminds me of another question. Two brothers that were born virtually at the same time on the same day in the same year to the same parents are not twins. How can this be?

References

1. L. Bankoff, Are the Twin Circles of Archimedes Really Twin, Mathematics Magazine, Vol. 47, No. 4 (Sept., 1974), 214-218

Inversion - Introduction

• Angle Preservation Property
• Apollonian Circles Theorem
• Archimedes' Twin Circles and a Brother
• Bisectal Circle
• Chain of Inscribed Circles
• Circle Inscribed in a Circular Segment
• Circle Inversion: Reflection in a Circle
• Circle Inversion Tool
• Feuerbach's Theorem: a Proof
• Four Touching Circles
• Hart's Inversor
• Inversion in the Incircle
• Inversion with a Negative Power
• Miquel's Theorem for Circles
• Peaucellier Linkage
• Polar Circle
• Poles and Polars
• Ptolemy by Inversion
• Radical Axis of Circles Inscribed in a Circular Segment
• Steiner's porism
• Stereographic Projection and Inversion
• Tangent Circles and an Isosceles Triangle
• Tangent Circles and an Isosceles Triangle II
• Three Tangents, Three Secants
• Viviani by Inversion
• Simultaneous Diameters in Concurrent Circles

• Arbelos - the Shoemaker's Knife
• 7 = 2 + 5 Sangaku
• Another Pair of Twins in Arbelos
• Archimedes' Quadruplets
• Archimedes' Twin Circles and a Brother
• Book of Lemmas: Proposition 5
• Book of Lemmas: Proposition 6
• Chain of Inscribed Circles
• Concurrency in Arbelos
• Concyclic Points in Arbelos
• Ellipse in Arbelos
• Gothic Arc
• Pappus Sangaku
• Rectangle in Arbelos
• Squares in Arbelos
• The Area of Arbelos
• Twin Segments in Arbelos
• Two Arbelos, Two Chains
• A Newly Born Pair of Siblings to Archimedes' Twins

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

They were two of a set of triplets or quadraplets or ...

|Activities| |Contact| |Front page| |Contents| |Store| |Geometry|