Extremal Distance Ratio
Problem and Solution
GRÉGOIRE NICOLLIER
UNIVERSITY OF APPLIED SCIENCES OF WESTERN SWITZERLAND
ROUTE DU RAWYL 47, CH-1950 SION, SWITZERLAND
Given a line $\ell$ and two points $A$ and $B$ not on $\ell$, construct the points $X$ of $\ell$ that make the distance ratio $XA/XB$ extremal.
Solution 1
Here is a simpler solution than in [1].
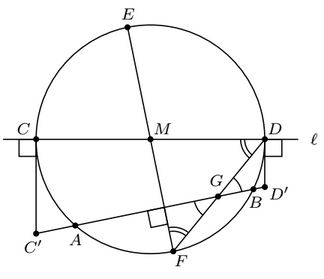
We suppose that $AB$ is not perpendicular to $\ell$ and construct the circle through $A$ and $B$ with diameter $CD$ on $\ell.$ We prove that $C$ and $D$ are the points $X$ we are looking for by considering $C'$ and $D'$ on the line $AB$ given $CC' \perp\ell\perp DD'.$
$DF$ is angle bisector of $\angle ADB$ by the inscribed angle theorem as
$\angle ADB = \angle AEB = 2\angle FEB = 2\angle FDB,$
thus $D$ and $G$ are on the same Apollonius circle $XA/XB = DA/DB$ by the angle bisector theorem. $GD' = DD'$ by angle chasing, hence $D'$ is the center of the above Apollonius circle. As the Apollonius circle is tangent to $\ell,$ $D$ maximizes $XA/XB$ under the constraint $X\in\ell.$
The proof is similar for the minimum at $C.$ For $AB\perp\ell,$ the solutions are the point at infinity of $\ell$ and the intersection with the line $AB$ (and possibly every point of $\ell).$
Solution 2
There is an even shorter proof. Each circle $XA/XB = const$ cuts all circles through $A$ and $B$ at right angles. We are looking for circles $XA/XB = const$ tangent to $\ell,$ that is, for circles through $A$ and $B$ that cut $\ell$ at right angles: we are done!
References
- A. Bialostocki and R. Ely, Points on a line that maximize and minimize the ratio of the distances to two given points, Forum Geom. 15 (2015) 177–178.
Elaboration
Let $U=rA+(1-r)B,$ for $r\in(0,1).$ There is a unique Apollonian circle $XA/XB=const$ that passes through $U.$ The ratio $UA/UB$ is a monotone function of the location of $U$ on $AB,$ or, which is the same, of $r.$ For small and large ratios, i.e., for $r$ near $0$ or $1,$ the circle does not intersect $\ell.$ For $r=1/2$ it degenerates into a perpendicular bisector of $AB.$
When an Apollonian circle is tangent to $\ell$ its radius to the point of tangency is perpendicular to $\ell.$ As this happens exactly twice, the two points of tangency define a diameter of an auxiliary circle, with the center at the intersection of $\ell$ and the perpendicular bisector of $AB.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73577140
