Locus of Points in a Given Ratio to Two Points

Given two points A and B and a number r. What is the locus of points P such that AP/BP = r?

Created with GeoGebra

Apollonian Circles Theorem

Given two points A and B and a number r. What is the locus of points P such that AP/BP = r?

The locus is a circle, unless of course r = 1, in which case it's the perpendicular bisector of AB. The proof exploits the properties of angle bisectors: internal and external.

To see that (there is an additional proof), construct points M and N on the line AB such that AM/BM = AN/BN = r. For r ≠ 1, M and N always exist. Note that both M and N lie on the sought locus.

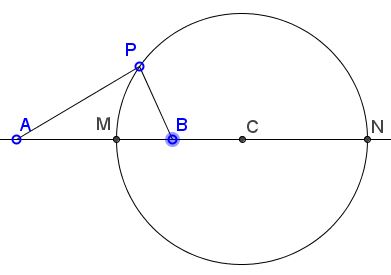
Apollonius' circle

The circle at hand has MN as a diameter. Indeed, M serves as the feet of the internal bisector of triangle APB at apex P, PN serves as the external bisector. Therefore, PM ⊥ PN. Chords PM and PN are perpendicular and therefore define a 90° inscribed angle. The angle subtends a 180° arc, which means that MN is a diameter of the circle.

For any P on the circle, the internal and external bisectors of angle APB pass through (the fixed points) M and N.

The circle we just constructed is known as a Circle of Apollonius. The family of all such circles obtained for different values of r and fixed points A and B is known as the Apollonian Family of Circles defined by the points A and B. Note that one of these circles (corresponding to r = 1) is actually a straight line. It is often convenient to think of straight lines together with common circles as generalized circles, circles of infinite and finite radii.

Since, for the same A and B, each of the Apollonian circles correponds to a different r, no two Apollonian circles intersect. For 0 < r < 1, the circles are closer to A and surround it. For smaller values of r, they are increasingly close to B. For r > 1, the circles surround B and, as r grows become increasingly close to it. For this reason, points A and B are often considered as circles, now point circles, circles of radius 0.

72202054