Two Squares In Circle
Source

Problem
Squares $ABCD\;$ and $EFGH\;$ are inscribed in a circle, forming in intersection an octagon $MNPQRSTU.$
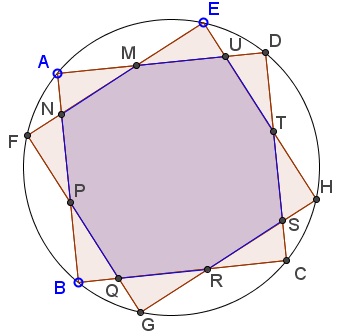
Prove that $[MNPQRSTU]\ge 2(\sqrt{2}-1)[ABCD],\;$ where $[\mathcal{X}]\;$ denotes the area of figure $\mathcal{X}.$
Proof 1
WLOG, assume that the squares have side $1.\;$ If $x=[MNPQRSTU],\;$ then $2x=2-[\text{the eight triangles}].\;$ The minor arcs ${AB}$ and ${EF}$ are equal, so that $AB=EF,\;$ making $AEBF\;$ an isosceles trapezoid. It follows that $\Delta NAF\;$ is isosceles and $NA=NF.\;$ Since triangles $NFP\;$ and $NAM\;$ are similar, we deduce that they are in fact congruent. Thus all eight triangles are congruent.
We denote $AN=a\sin t,\;$ $\displaystyle 0\lt t\lt\frac{\pi}{2}.$ This implies that $NP=a\;$ and $PB=a\cos t\;$ from which $a=\displaystyle\frac{1}{1+\sin t+\cos t}.\;$ Thus
$[\text{the eight triangles}]=\displaystyle\frac{4\sin t\cos t}{(1+\sin t+\cos t)^2}.\;$
If $\sin t+\cos t=y,\;$ $2\sin t\cos t=y^2-1\;$ and $a\lt y\le\sqrt{2}.$ From here,
$\displaystyle\frac{4\sin t\cos t}{(1+\sin t+\cos t)^2}=\frac{2(y^2-1)}{(y+1)^2}=\frac{2(y-1)}{y+1}\le\frac{2(\sqrt{2}-1)}{\sqrt{2}+1}$
so that $[\text{the eight triangles}]\le 2(3-2\sqrt{2}),\;$ $2x\ge 2-2(3-2\sqrt{2}),\;$ or $x\ge 2(\sqrt{2}-1).$
Proof 2
By symmetry, the four cut-off triangles of either square are equal. By the Carpets Theorem, the sum of the ares of the cut-off triangles of one of the squares equals to the sum of the areas of the others. It follows that all eight triangles are equal.
Let $x=AM=ME,\;$ $y=EU=UD,\;$ $MU=z.\;$ WLOG, assume $x+y+z=1.\;$ By the Pythagorean Theorem, $x^2+y^2=z^2=(1-x-y)^2,$ which is equivalent to $\displaystyle (1-x)(1-y)=\frac{1}{2}.\;$ By the AM-GM inequality,
$\displaystyle \frac{(1-x)+(1-y)}{2}\ge\sqrt{(1-x)(1-y)}=\frac{1}{\sqrt{2}},$
or, $x+y\le 2-\sqrt{2}.$ On the other hand, $\displaystyle (1-x)(1-y)=\frac{1}{2}\;$ is equivalent to $\displaystyle xy=x+y-\frac{1}{2},\;$ implying that $\displaystyle xy\le\frac{3}{2}-\sqrt{2}.$ But $xy=2[\text{one of the triangles}].\;$ So that $\displaystyle [\text{the eight triangles}]\le 2(3-2\sqrt{2}),\;$ and, subsequently, $[MNPQRSTU]\ge 2(\sqrt{2}-1).$
Note that the minimum is achieved when $x=y.$
Acknowledgment
The problem which is due to Miguel Ochoa Sanchez has been posted by Leo Giugiuc at the CutTheKnotMath facebook page along with a solution (Proof 1) by Dan Sitaru and Leo Giugiuc.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73592762
