The Carpets Theorem
What is it about?
A Mathematical Droodle

Created with GeoGebra

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet is supposed to illustrate a simple fact that in various guises helps solve problems that otherwise may require a serious effort. In the applet, the total area of the red regions always equals that of the blue region. (So as to avoid possible ambiguity, all the regions in the applet are drawn inside the square ABCD.)

In some instances, this is exceedingly clear.

In the diagram there are two triangles - BMD and BMC - that share the base BM and the altitude (DA = CB). They have equal areas. If we remove from both triangles their intersection BMR, then the remaining regions, viz., triangles DMR and BCR will have equal areas:

Area(DMR) = Area(BCR);

This is just a consequence of a property of addition:

a + c = b + c implies
a = b

and additivity of area:

Area(BMD) = Area(DMR) + Area(BMR) and
Area(BMC) = Area(BCR) + Area(BMR).

(We have actually established an important property of trapezoids: the two out of four triangles formed by the diagonals of a trapezoid that are adjacent to its sides have equal areas. This property is used elsewhere.)

We can state a variant of the Carpets Theorem:

If two carpets of equal area overlap, then, the overlap aside, their remaining parts have equal areas.

As an application, consider the diagram below.

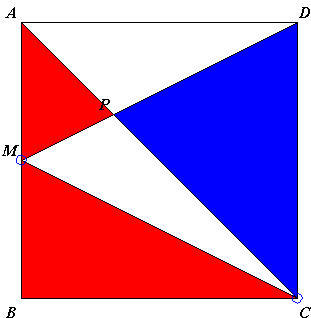
Two triangles - ABC and CDM - of equal area, intersect in triangle MPC. We conclude that their remaining parts total equal areas:

Area(CDP) = Area(AMP) + Area(BCM).

(In passing, we also have Area(ADP) = Area(CMP), because triangles ACD and MCD have equal areas.)

A seemingly more difficult problem is presented by a more general case: point M is on the side AB, point N on the side BC. (Often they are taken to be the midpoints of the sides, but the result does not depend on their specific location.) Prove that the total of red areas equals that of the blue area, as claimed.

We get the necessary result by considering two shapes of equal area: one is triangle ADN, the other is the union of triangles ADM and BCM. Both shapes cover half the square ABCD. Their intersection is the union of triangles ADP and NQR. The blue area is what remains of ΔADN. The red area is what remains of ΔADM ∪ ΔBCM:

Area(DPQR) = Area(AMP) + Area(BMQN) + Area(CNR).

The Carpets Theorem owes its name to a different formulation. Let a floor in a room be completely covered by carpet pieces with no overlap. Moving one of the pieces on one hand creates an overlap and on the other uncovers a portion of the floor. The theorem states the obvious fact that the two areas so obtained are equal.

The two formulations are obviously equivalent. In order to obtain the former from the latter we have to consider two regions occupied by the piece that has been moved, before and after its displacement.

Assume now we have a shape U split into two halves (i.e. equal in area) in two ways:

(1)	U = S1 ∪ S2 = T1 ∪ T2

and

(2)	Area(S1) = Area(S2) = Area(T1) = Area(T2) = Area(U)/2,

then

(3)	Area(S1 ∩ T1) = Area(S2 ∩ T2).

In other words, if (1) and (2) hold then the second formulation is strangely strengthened. Namely, the piece that moved and the area it uncovered need not be of the same shape! The proof is straightforward.

T₁ = S₁∩T₁ ∪S₂∩T₁,

from which

S₁∩T₁ = T₁ - S₂∩T₁.

And in terms of areas

(4)	Area(S1∩T1) = Area(T1) - Area( S2∩T1).

Similarly

(5)	Area(S2∩T2) = Area(S2) - Area( S2∩T1).

Since Area(T₁) = Area(U)/2 = Area(S₂), (3) follows from (4) and (5).

Now, if you examine carefully the last step, then it becomes clear that we have not used the full set of equalities in (2), but only Area(T₁) = Area(S₂). Thus we actully proved a more general statement:

We have an immediate application for the latest generalization.

References

1. T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004

Carpets Theorem

• The Carpets Theorem
• Carpets in a Parallelogram
• Carpets in a Quadrilateral
• Carpets in a Quadrilateral II
• Square Root of 2 is Irrational
• Carpets Theorem With Parallelograms
• Two Rectangles in a Rectangle
• Bisection of Yin and Yang
• Carpets in Hexagon
• Round Carpets
• A Property of Semicircles
• Carpets in Triangle
• Carpets in Triangle, II
• Carpets in Right Triangle
• Piecewise Carpets in Parallelogram

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny