Optimal Quadrilateral Inscribed in a Square

An interesting optimization problem has been offered by Dan Sitaru at the CutTheKnotMath facebook page:

$x,y,z,t\in(0,1).$ $\Omega=\sum_{cycl}\sqrt{x^2+(1-y)^2}.$ Find $m=\inf\Omega$ and $M=\sup\Omega.$

We'll use complex numbers.

The function $f:\;[0,1]^{4}\rightarrow\mathbb{R},$ defined by $f(x,y,z,t)=\displaystyle\sum_{cycl}\sqrt{x^2+(1-y)^2},$ is continuous and thus attains its extrema on $[0,1]^{4}.$ The extremal values on $[0,1]^{4}$ will supply its supremum and infimum on $(0,1)^{4}.$

Let's look for infimum first. $\sqrt{x^2+(1-y)^2}=|x+i(1-y)|,$ etc. By the triangle inequality,

$\begin{align} \displaystyle\sum_{cycl}\sqrt{x^2+(1-y)^2} &=\sum_{cycl}|x+i(1-y)|\\ &\ge|(x+y+z+t)+i[4-(x+y+z+t)]|\\ &=|k+i(4-k)|, \end{align}$

where $k=x+y+z+t,$ $0\le k\le 4.$ But $|k+i(4-k)|=\sqrt{k^2+(4-k)^2}\ge 2\sqrt{2}$ which is attained with $k=2,$ in particular when $x=y=z=t=\frac{1}{2}.$ Thus, $m=\inf\Omega=2\sqrt{2}.$

To find the supremum, observe that, for real $a$ and $b,$ $\sqrt{a^2+b^2}\le |a|+|b|,$ with equality only when $ab=0.$ In our case,

$\displaystyle\sum_{cycl}\sqrt{x^2+(1-y)^2} \le\sum_{cycl}(x+1-y)=4.$

This is attained with $x=y=z=t=0.$ Thus, $m=\sup\Omega$=4.

Let the square be of side length 1 and an inscribed quadrilateral $ABCD$ with sides $a,$ $b,$ $c,$ $d,$ as shown below:

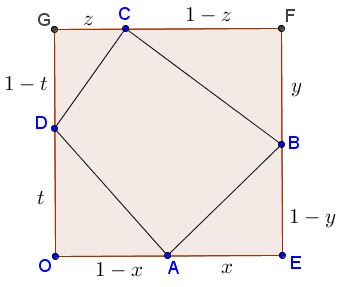
Then, for example, $a^2=x^2+(1-y)^2,$ etc. Thus

$\displaystyle\begin{align} \sum_{cycl}a^2&=\sum_{cycl}(x^2+(1-x)^2)\\ &=\sum_{cycl}\left[2(x-\frac{1}{2})^2+\frac{1}{2}\right]. \end{align}$

But, for $x\in [0,1],$ $\displaystyle 1\ge 2(x-\frac{1}{2})^2+\frac{1}{2}\ge\frac{1}{2},$ implying

$2\le a^2+b^2+c^2+d^2 \le 4.$

For the perimeter,

$\displaystyle\begin{align} \sum_{cycl}a&\le\sum_{cycl}[x+(1-y)]\\ &=\sum_{cycl}[x+(1-x)]\\ &= 4. \end{align}$

By the Chebyshev inequality,

$\displaystyle 2\cdot\frac{1}{4}\le \frac{1}{4}\sum_{cycl}a^2\le\left(\frac{1}{4}\sum_{cycl}a\right)^2,$

From which $\displaystyle\left(\frac{1}{4}\sum_{cycl}a\right)^2\ge\frac{1}{2},$ or $\displaystyle\sum_{cycl}a\ge 2\sqrt{2}.$

The low bound can be determined also with the remark (that is related to Solution 3) that the perimeter of $ABCD$ is minimal if it's a closed light path. All of these light polygons have the same perimeter $2\sqrt{2},$ which is twice the length of a diagonal. Hence, $a+b+c+d\ge 2\sqrt{2}.$

Solution 1 is by Leo Giugiuc. Solution 2 is from A. Engel, Problem-Solving Strategies (Springer Verlag, 1998, p. 190).

Another solution - a proof without words - due to Grégoire Nicollier appears on a separate page.