Optimal Quadrilateral Inscribed in Square, PWW

What Is This About?

Problem

Inscribe in a given square $OEFG$ quadrilateral $ABCD$ of minimal perimeter such that $A\in OE,$ $B\in EF,$ $C\in FG,$ $D\in GO.$

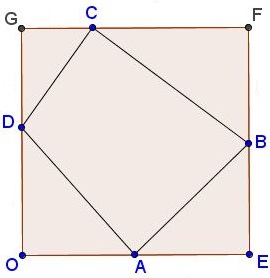
Optimal Quadrilateral Inscribed in Square, PWW - problem

Solution

With three reflections (in $OE,$ $OD,$ and the line $CD),$ we obtain two points $B'$ and $B'''$ - reflections of $B$ - that are joined by a broken line $B'ADC'B'''$ whose length equals the perimeter of the quadrilateral $ABCD.$

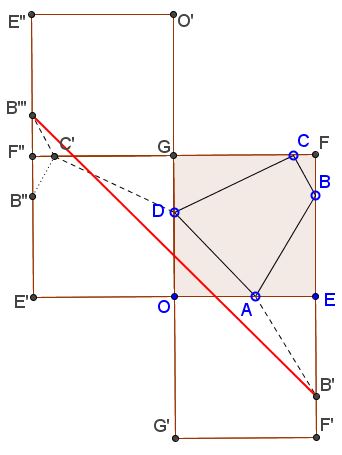
Optimal Quadrilateral Inscribed in Square, PWW - step 1

By manipulating points $A,$ $C,$ and $D$, one can straighten the broken line into a straight line segment $B'B'''$ parallel to the diagonal $EG$ of the given square and equal twice its length: $|B'B'''|=2\sqrt{2},$ assuming the square of unit side length.

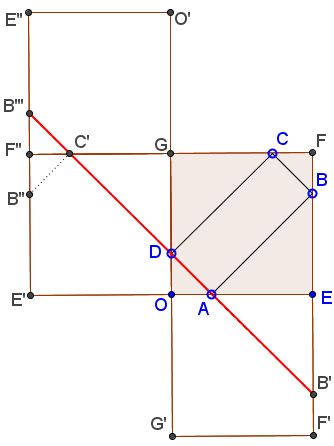
Optimal Quadrilateral Inscribed in Square, PWW - step 2

It is clear that the solution is not unique: to any position of point $B$ on side $EF$ there exists a rectangle with the sides parallel to the diagonals of $OEFG$ and, therefore, perimeter equal $2\sqrt{2}.$

Acknowledgment

The above came in a comment by Grégoire Nicollier to an algebraic variant of the current problem. Grégoire observed that the generalization to the case of a rectangular $OEFG$ is immediate.

73236352