Properties of Flank Triangles

Bottema's configurationof two squares that share a vertex is naturally embedded into Vecten's configuration of three squares erected on the sides of a triangle. The latter generalizes the first of Euclid's proofs of the Pythagorean theorem, so it rightfully refers to the Bride's Chair.

In the discussion of Vecten's configuration, we proved inter alia two properties of flank triangles that are a part of Bottema's configuration.

  1. Continuation of a median (altitude) from the common vertex in one flank triangle form the altitude (median) in the other.

  2. The base opposite the common vertex in one flank triangle is twice as long as the median from the common vertex in the other.

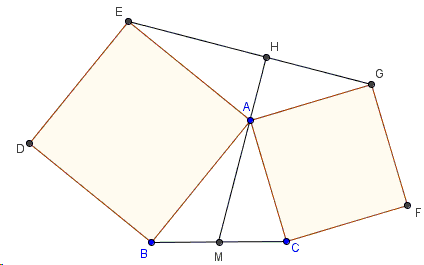
two properties of the flank triangles - flanks

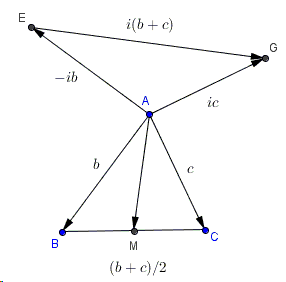
With a reference to the diagram,

  1. If \(AM\) is a median in \(\triangle ABC\), \(AH\) is an altitude in \(\triangle AEG\), then \(M\), \(A\), \(H\) are collinear.

  2. \(EG = 2\cdot AM\).

I'll give five proofs of these properties, three using rotation transform, one with complex variables, and one with an extra construction that has the virtue of revealing an additional property of Bottema's configuration. All five proofs qualify as proofs without words, however, I placed a dynamic demonstration of each on a separate page.

Proof 1

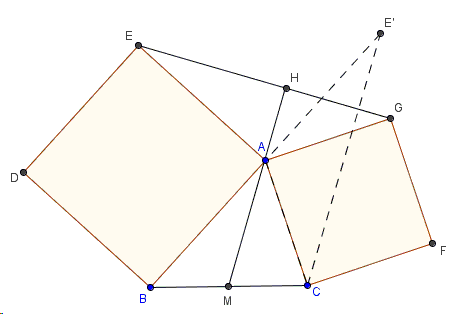
two properties of the flank triangles - first proof by symmetric rotation

Proof 2

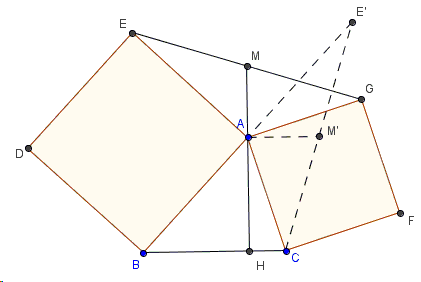
two properties of flank triangles - second proof by symmetric rotation

Proof 3

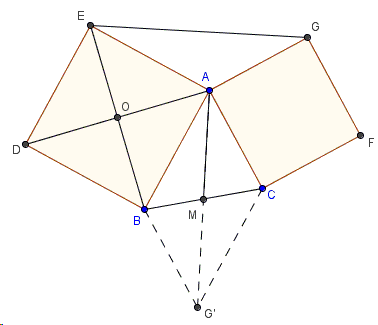
wo properties of Bottema's configuration - asymetric rotation

Proof 4

two properties of the flank triangles - proof with comlex variables

Proof 5

two properties of the flank triangles - a parallelogram proof

Bottema's Theorem

  1. Bottema's Theorem
  2. An Elementary Proof of Bottema's Theorem
  3. Bottema's Theorem - Proof Without Words
  4. On Bottema's Shoulders
  5. On Bottema's Shoulders II
  6. On Bottema's Shoulders with a Ladder
  7. Friendly Kiepert's Perspectors
  8. Bottema Shatters Japan's Seclusion
  9. Rotations in Disguise
  10. Four Hinged Squares
  11. Four Hinged Squares, Solution with Complex Numbers
  12. Pythagoras' from Bottema's
  13. A Degenerate Case of Bottema's Configuration
  14. Properties of Flank Triangles
  15. Analytic Proof of Bottema's Theorem
  16. Yet Another Generalization of Bottema's Theorem
  17. Bottema with a Product of Rotations
  18. Bottema with Similar Triangles
  19. Bottema in Three Rotations
  20. Bottema's Point Sibling

|Contact| |Front page| |Content| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72187084