On Bottema's Shoulders with a Ladder

What is this about?

Problem

Segment $AB$ is fixed. $ACA'$ and $BCB'$ are similar isosceles ($AC=A'C$ and $BC=B'C$) triangles, with a given apex angle. $D$ is the intersection of the bisector of $\angle ACA'$ with the circumcircle $(ACA'),$ $E$ the intersection of the bisector of $\angle BCB'$ with the circumcircle $(BCB').$ $(ACA')$ and $(BCB')$ meet at $J$. $G$ is the midpoint of $DE.$

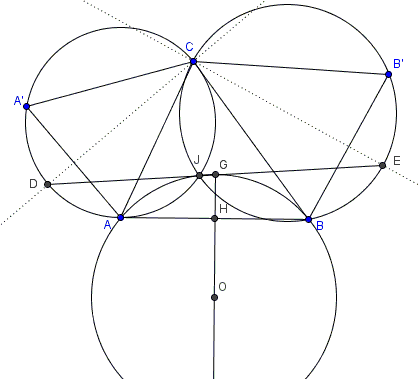
A generalization of Bottema's theorem

Prove that

$D,$ $J,$ and $E$ are collinear,
$AB',$ $A'B$ meet at $J,$
$AB'=A'B,$
$CJ$ is the bisector of $\angle AJB,$
If $O_A,$ $O_B$, $O$ are the centers of $(ACA'),$ $(BCB'),$ and $(AGB),$ respectively, then $OO_A=OO_B$ and triangle $O_{A}OO_B$ is similar to triangles $ACA'$ and $BCB'.$
Position of $G$ is independent of $C,$
Quadrilateral $AJGB$ is cyclic and $G$ is the midpoint of arc $AB.$

Hint

You may start with chasing inscribed angles.

Solution

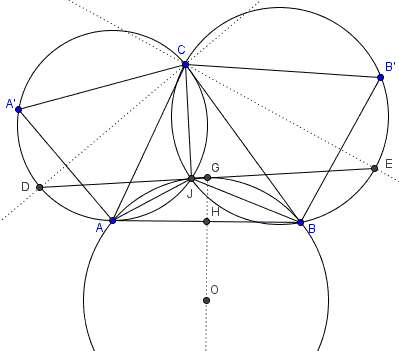
A generalization of Bottema's theorem - solution, step 1

Let $\alpha = \angle CAA' = \angle CA'A = \angle CBB' = \angle CB'B\space$ and $\beta = \angle ACA'=\angle BCB'$ such that $2\alpha +\beta =180^{\circ}.$ Then, $\angle CJD$ equals half the arc $CD=CA'+A'D,$ making $\angle CJD=\alpha +\beta/2.$ Similarly, $\angle CJE=\alpha +\beta/2.$ Thus each of these angles is right and together they give $180^{\circ},$ meaning that $D,$ $J,$ and $E$ are collinear (#1). (As a byproduct, $CD$ is a diameter in $(ACA'),$ $CE$ is a diameter in $(BCB').)$

$\angle A'JC=\alpha$ while $\angle BJC=\alpha+\beta$ so again $\angle A'JC+\angle BJC=2\alpha+\beta=180^{\circ},$ implying that $A',$ $J,$ and $B$ are collinear. Similarly, $A,$ $J,$ and $B'$ are collinear (#2).

$\angle A'CB=\angle A'CA+\angle ACB=\angle B'CB+\angle ACB=\angle ACB',\space$ implying that triangles $A'CB$ and $ACB'$ are equal by SAS so that also $AB'=A'B$ (#3).

$\angle AJD = \beta/2 = \angle BJE$ while $CJ\perp DE,$ proving #4. $\angle AJB = 2\alpha,$ making each half equal $\alpha.$

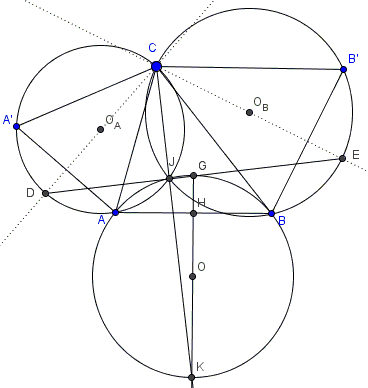
A generalization of Bottema's theorem - solution, step 2

To prove #5, note that $O_AO_B\perp CJ$ while $OO_A\perp AJ$ which says that $\angle OO_AO_B=180^{\circ}-\angle AJC=90^{\circ}-\beta/2=\alpha.$ Similarly, $\angle OO_BO_A=\alpha.$

(Hubert Shutrick came up with a triginometric proof of ##6-7.) Denoting the angles of $\Delta ABC$ $\bar{\alpha},$ $\bar{\beta},$ and $\bar{\gamma},$ and the sides $a,$ $b,$ and $c,$ let $D'$ and $E'$ on $AB$ be projections of $D$ and $E.$ Observe that, since $CD$ is a diameter of $(O_A),$ $\angle CAD=90^{\circ},$ implying $\angle DAD'+\alpha=90^{\circ}$

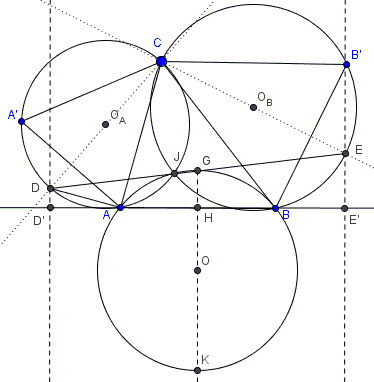
A generalization of Bottema's theorem - solution, step 3

$AD=a\space\mbox{tan}(\beta/2)$ and $AD'=AD\space\mbox{sin}(\bar{\alpha})$ which together give $AD' = a\space\mbox{tan}(\beta/2)\mbox{sin}(\bar{\alpha}).$ Similarly, $BE'= b\space\mbox{tan}(\beta/2)\mbox{sin}(\bar{\beta}).$ But both $a\space\mbox{sin}(\bar{\alpha})$ and $b\space\mbox{sin}(\bar{\beta})$ express the length of $C$-height in $\Delta ABC.$ Therefore, $AD'=BE'.$

If the midpoint of $AB$ is $H,$ then (from the above) $D'H=E'H$ and also

$2GH = a\space\mbox{tan}(\beta/2)\mbox{cos}(\bar{\alpha}) + b\space\mbox{tan}(\beta/2)\mbox{cos}(\bar{\beta}) = AB\space\mbox{tan}(\beta/2).$

Thus, $\angle GAB = \beta/2 = \angle GJB,$ proving #6. #7 follows from the fact that $\angle AJB = 2\alpha = \angle AGB.$

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

Bottema's Theorem

72104951