Properties of Flank Triangles - Proof with an Asymmetric Rotation
Bottema's configuration of two squares that share a vertex is naturally embedded into Vecten's configuration of three squares erected on the sides of a triangle. The latter generalizes the first of Euclid's proofs of the Pythagorean theorem, so it rightfully refers to the Bride's Chair.
In the discussion of Vecten's configuration, we proved inter alia two properties of flank triangles that are a part of Bottema's configuration.
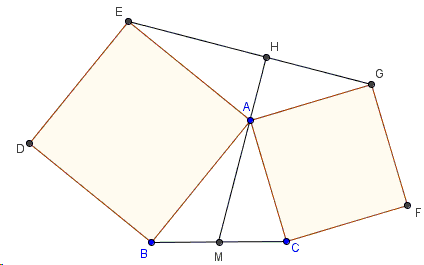
If \(AM\) is a median in \(\triangle ABC\), \(AH\) is an altitude in \(\triangle AEG\), then \(M\), \(A\), \(H\) are collinear.
\(EG = 2\cdot AM\).
The applet below illustrates one of the solutions. Use the slider at the top of the applet to rotate \(\triangle AEG\) \(90^{\circ}\) clockwise around \(O\) - the center of square \(ABDE\).
Proof
The rotation around \(O\) maps \(E\) to \(A\), \(A\) to \(B\), and \(G\) to \(G'\) such that the quadrilateral \(ABG'C\) is a parallelogram. (This is because \(BG'\parallel AC\) and \(BG' = AG = AC\).) So naturally, \(AM\) is half the diagonal \(AG' = EG\).
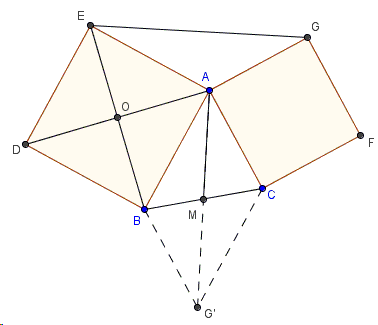
Also, by the construction, \(AG'\perp EG\) and the same holds for \(AM\): \(AM\perp EG\).
References
- R. Honsberger, Mathematical Diamonds, MAA, 2003, 63-64
Properties of Flank Triangles
- Bottema's Theorem
- A Degenerate Case of Bottema's Configuration
- Properties of Flank Triangles
- Two Properties of Flank Triangles - First Proof by Symmetric Rotation
- Properties of Flank Triangles - Second Proof by Symmetric Rotation
- Properties of Flank Triangles - Proof with an Asymmetric Rotation
- Two Properties of Flank Triangles - A Proof with Complex Numbers
- Two Properties of Flank Triangles - and a Third One
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73578551
