Bottema with Similar Triangles
What Might This Be About?
Problem
Assume triangles $BET,$ $DAT,$ and $DFC$ are similar as shown below.
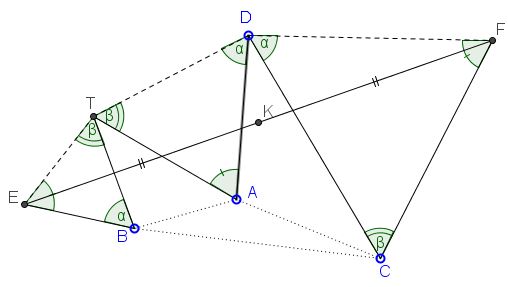
Prove that $K,$ the midpoint of $EF$ is independent of the position of $D.$
Solution

Assuming the point names as complex numbers, the similarity of the three triangles could be expressed as
$\displaystyle\frac{T-E}{B-E}=\frac{T-A}{D-A}=\frac{C-F}{D-F}=u,$
for a complex number $u.$ From here,
$\displaystyle\frac{(T+C)-(E+F)}{(B+D)-(E+F)}=u,$
implying
$\displaystyle\frac{(A+C)-(E+F)}{(A+B)-(E+F)}=u,$
which exactly means that $E+F$ and, with it, $\displaystyle\frac{E+F}{2}$ is independent of $D.$
Acknowledgment
This problem is a follow-up of the one posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. The simple solution above has been posted by Leo Giugiuc (Romania) who also observed that Dao's problem extends to the one above. Here's Dao's formulation:
Triangles $BET,$ $TAD,$ $DFC$ are similar isosceles. Prove that the midpoint $K$ of $EF$ is independent of the position of $D.$
Bottema's Theorem
- Bottema's Theorem
- An Elementary Proof of Bottema's Theorem
- Bottema's Theorem - Proof Without Words
- On Bottema's Shoulders
- On Bottema's Shoulders II
- On Bottema's Shoulders with a Ladder
- Friendly Kiepert's Perspectors
- Bottema Shatters Japan's Seclusion
- Rotations in Disguise
- Four Hinged Squares
- Four Hinged Squares, Solution with Complex Numbers
- Pythagoras' from Bottema's
- A Degenerate Case of Bottema's Configuration
- Properties of Flank Triangles
- Analytic Proof of Bottema's Theorem
- Yet Another Generalization of Bottema's Theorem
- Bottema with a Product of Rotations
- Bottema with Similar Triangles
- Bottema in Three Rotations
- Bottema's Point Sibling
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73614995
