Analytic Proof of Bottema's Theorem

Consider a configuration of two squares ACBcBa and BCAcAb with a common vertex C.

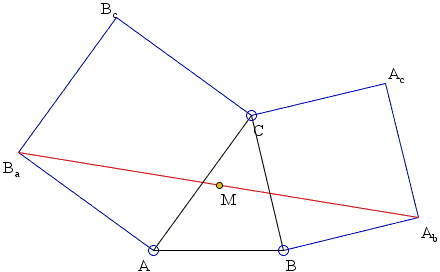
Bottema's theorem

Bottema's theorem claims that the midpoint M of the segment AbBa is independent of C.

Proof

A short analytic proof by Hubert Shutrick demonstrates how simple the theorem actually is.

If \(A = (-1,0)\), \(B = (1,0)\) and \(C = (x,y)\), then \(A_b = (y+1, 1-x)\), \(B_a = (-1-y, 1+x)\) and their midpoint is \((A_{b} + B_{a})/2 = (0,1)\).

Moreover, the proof makes it rather obvious that the angle \(AMB\) is right and, therefore, is the center of the square erected on \(AB\) on the side of \(C\).

As a practice in analytic geometry we may elaborate on the above diagram:

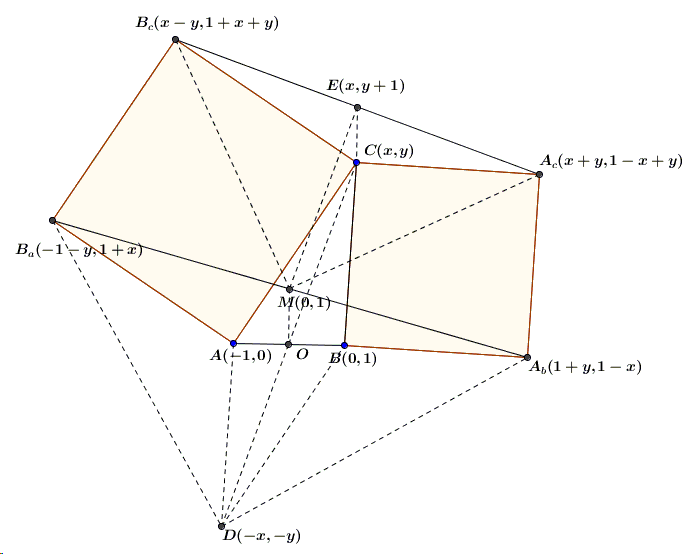
Bottema's theorem

As Hubert Shutrick has observed, \(\triangle A_{c}MB_{c}\) is right isosceles. He also noticed that \(OECM\), where \(E\) is the midpoint of \(A_{c}B_{c}\), is a parallelogram. Analytic geometry helps confirm another fact, the one noticed by William McWorter, viz., \(\triangle A_{b}B_{a}D\) is also right isosceles.

Bottema's Theorem

  1. Bottema's Theorem
  2. An Elementary Proof of Bottema's Theorem
  3. Bottema's Theorem - Proof Without Words
  4. On Bottema's Shoulders
  5. On Bottema's Shoulders II
  6. On Bottema's Shoulders with a Ladder
  7. Friendly Kiepert's Perspectors
  8. Bottema Shatters Japan's Seclusion
  9. Rotations in Disguise
  10. Four Hinged Squares
  11. Four Hinged Squares, Solution with Complex Numbers
  12. Pythagoras' from Bottema's
  13. A Degenerate Case of Bottema's Configuration
  14. Properties of Flank Triangles
  15. Analytic Proof of Bottema's Theorem
  16. Yet Another Generalization of Bottema's Theorem
  17. Bottema with a Product of Rotations
  18. Bottema with Similar Triangles
  19. Bottema in Three Rotations
  20. Bottema's Point Sibling

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72354314