An Elementary Proof of Bottema's Theorem

Consider a configuration of two squares ACBcBa and BCAcAb with a common vertex C.

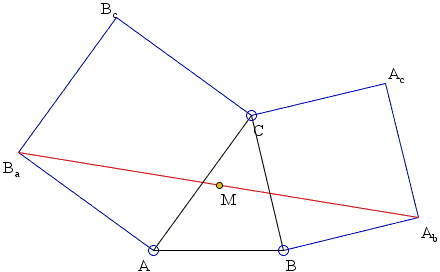
Bottema's theorem

Bottema's theorem claims that the midpoint M of the segment AbBa is independent of C.

Proof

Let's drop perpendiculars BaU, MW, AbV, and CZ onto AB.

An Elementary Proof of Bottema's Theorem

MW is the midline of trapezoid BaUVAb so that

MW = (BaU + AbV) / 2.

Further, since ∠BaAC is right, angles BaAU and CAZ are complementary which makes right triangles BaAU and ACZ equal, implying

BaU = AZ.

Similarly,

AbV = BZ.

Taking all three identities into account shows that

MW = (BaU + AbV) / 2 = (AZ + BZ) / 2 = AB/2 = AW,

independent of C. (The proof also shows that M is the center of the square formed on AB upwards.)

Note: there is a dynamic illustration of the proof that makes it entirely obvious.

Reference

  1. A. Shriki, Back To Treasure Island, MathematicS Teacher, Vol. 104, No. 9 (May 2011), 658-664

Bottema's Theorem

  1. Bottema's Theorem
  2. An Elementary Proof of Bottema's Theorem
  3. Bottema's Theorem - Proof Without Words
  4. On Bottema's Shoulders
  5. On Bottema's Shoulders II
  6. On Bottema's Shoulders with a Ladder
  7. Friendly Kiepert's Perspectors
  8. Bottema Shatters Japan's Seclusion
  9. Rotations in Disguise
  10. Four Hinged Squares
  11. Four Hinged Squares, Solution with Complex Numbers
  12. Pythagoras' from Bottema's
  13. A Degenerate Case of Bottema's Configuration
  14. Properties of Flank Triangles
  15. Analytic Proof of Bottema's Theorem
  16. Yet Another Generalization of Bottema's Theorem
  17. Bottema with a Product of Rotations
  18. Bottema with Similar Triangles
  19. Bottema in Three Rotations
  20. Bottema's Point Sibling

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

73362839