Bottema's Point Sibling

Created with GeoGebra

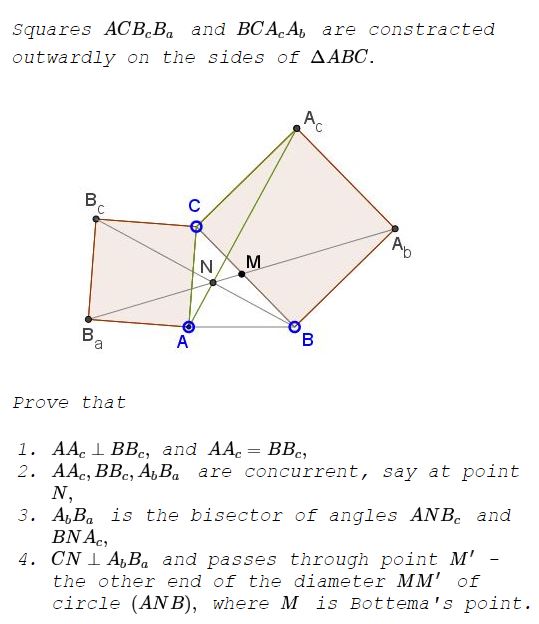
1. We prove that triangles $BCB_c\,$ and $A_cCA\,$ are equal. (Thus $AA_c=BB_c,$ as a consequence.) Indeed, $CB_c=CA,\,$ $CA_c=CB,\,$ and $\angle BCB_c=90^{\circ}+\angle ACB=\angle ACA_c.\,$ One is obtained from the other with a rotation through $90^{\circ}\,$ around point $C,\,$ making corresponding sides perpendicular. In particular, $AA_c\perp BB_c.$ Let $N\,$ be the intersection of the two.

2. Let $M\,$ be Bottema's point. Among the many properties it has, $M\,$ lies on the circle with diameter $AB.\,$ Since $\angle ANB=90^{\circ},\,$ $N\,$ lies on the same circle. $M\,$ is known to divide the arc $\overset{\frown}{AB}\,$ to which it belongs in half. This means that the arc $overset{\frown}{BM}\,$ is one quarter of the circle, making inscribed $\angle BNM=45{\circ}.$

   

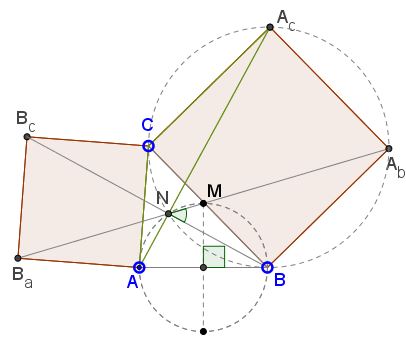
   $N\,$ also belongs to the circle $(CBA_bA_c)\,$ because $\angle BNA_c=90^{\circ}\,$ and $BA_c\,$ is a diameter of that circle. Inscribed $\angle BNA_b=45^{\circ}\,$ for it too is subtended by a quarter of a circle. Thus $M\,$ lies on $NA_b.$

   

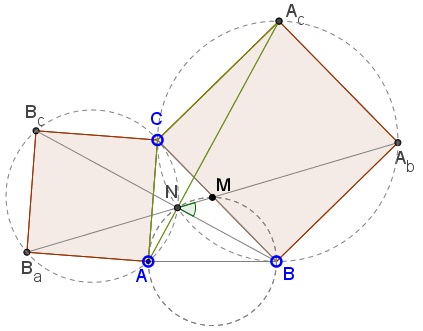
   Similarly, $N\in (ACB_cB_a)\,$ and, for that reason, $\angle ANB_a=45^{\circ},\,$ implying that A_bNB_a is a straight line. Thus the three lines $AA_c,BB_c,A_bB_a\,$ are indeed concurrent and

3. $A_bB_a\,$ is the bisector of angles $ANB_c\,$ and $BNA_c,$

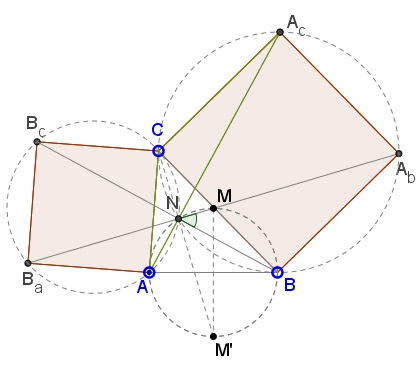
4. Inscribed $angle CNA_b=90^{\circ},\,$ as inscribed and subtended by the diameter $CA_b.\,$ If $M'\,$ is the second intersection of $CN\,$ with $(ANB),\,$ $\angle MNM'=90^{\circ},\,$ making $MM'\,$ a diameter of $(ANB).$

   

The problem has been tweeted by Antonio Gutierrez and introduced with a GeoGebra applet by Tim Brzezinski.

The configuration is a part of Vecten's construction involving squares on each side of a triangle that is known as Bride's chair. Here we relate it to the famous Bottema's problem.