Bottema's Theorem - Proof Without Words
If squares are constructed on the sides \(AC\) and \(BC\) of a triangle, then the midpoint \(M\) of the segment joining the vertices of the squares that are diagonally opposite \(C\) is independent of position of \(C\).
The applet illustrates an extra construction that makes Bottema's theorem rather obvious. Both the construction and the applet are due to Hubert Shutrick.
What do you see in this construction? Which conclusion did the illustration suggest? I find it curious that what I saw in the illustration was somewhat different from what Hubert intended to lay bare. For the sake of reference I'll describe the construction:
Drop perpendiculars \(EJ\), \(GK\), and \(CH\) to \(AB\). Note that \(CH=BK=AJ\) (This is because \(\Delta BCH=\Delta CBK\) and \(\Delta ACH=\Delta EAJ\).)
Extend \(EJ\) by \(EN=GK\) and \(GK\) by \(GP=EJ\). The resulting shape \(JKPN\) is a rectangle.
Let \(M\) be the center of the rectangle.
Now, Hubert continues with the assertion that,
\(\Delta BMA \) is isosceles with a right angle at \(M\). It follows that \(M\) forms a right-angled isosceles triangle with the other two vertices also.
Why so? Because, \(AJ=BK\), implying that \(M\) projects onto the midpoint of \(AB\) and, in addition, is at half the height of, say, \(KP\), but
\(KP = GK+GP = BH+AH=AB,\)
such that the distance from \(M\) to \(AB\) is half \(AB\), making indeed \(\Delta BMA \) isosceles with \(\angle AMB\) right.
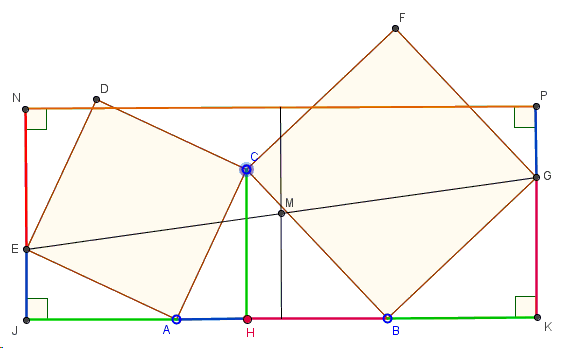
To me the diagram has communicated a somewhat different vision. Any rectangle has central symmetry (rotation through \(180^\circ\)) around its center. By the construction, \(EN=GK\), implying that \(E\) and \(G\) are images of each other under that central symmetry, making \(EMG\) a straight line, i.e., asserting that \(M\) serves the midpoint of \(EG\). It is independent of the position of \(C\) for the same reason as given by Hubert.
Bottema's Theorem
- Bottema's Theorem
- An Elementary Proof of Bottema's Theorem
- Bottema's Theorem - Proof Without Words
- On Bottema's Shoulders
- On Bottema's Shoulders II
- On Bottema's Shoulders with a Ladder
- Friendly Kiepert's Perspectors
- Bottema Shatters Japan's Seclusion
- Rotations in Disguise
- Four Hinged Squares
- Four Hinged Squares, Solution with Complex Numbers
- Pythagoras' from Bottema's
- A Degenerate Case of Bottema's Configuration
- Properties of Flank Triangles
- Analytic Proof of Bottema's Theorem
- Yet Another Generalization of Bottema's Theorem
- Bottema with a Product of Rotations
- Bottema with Similar Triangles
- Bottema in Three Rotations
- Bottema's Point Sibling
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73559549
