On Bottema's Shoulders
What Is This About?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Buy this applet What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2015 Alexander Bogomolny

On Bottema's Shoulders

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Buy this applet What if applet does not run?

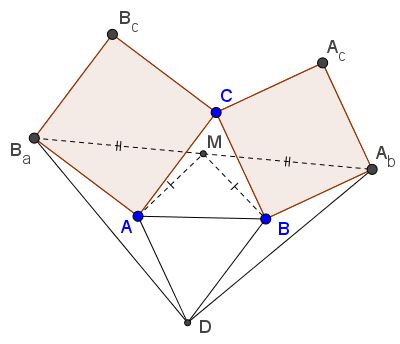
Consider a configuration of two squares ACB_cB_a and BCA_cA_b with a common vertex C. Bottema's theorem states that the midpoint M of the segment A_bB_a is independent of C. Professor W. McWorter has observed another property of the configuration: if D is the point that completes the parallelogram ADBC, then ΔB_aDA_b is isosceles and angle D is right: ∠B_aDA_b = 90°.

The theorem is easily proved with complex numbers but also has a simple synthetic proof.

Continuing with the proof of Bottema's theorem, we assume that the vertices A, B, and C are represented by the complex numbers α, β, and γ, respectively. We found there that

	Ba = α + (γ - α)·i,
	Ab = β + (γ - β)·(-i),
	M = (α + β)/2 + (β - α)·i/2,

where i² = -1, as usual. We then obviously have

i(Ab - M) = -i(Ba - M).

Denoting the point M + i(A_b - M) by D,

D = M + i(Ab - M)   = M + (-γ + (α + β)/2 + i(α - β)/2)   = (α + β) - γ   = α + (β - γ).

The latter tells us that ADBC is a parallelogram.

The synthetic proofs starts with the observation that in triangles AB_aD and BDA_b,

ABa = BD and AD = BAb.

The angles between the equal sides are also equal, since both are found to be

360° - 90° - ∠A - ∠B,

the latter being the angles of ΔABC at vertices A and B, respectively.

By Bottema's theorem, the clockwise rotation around M through 90°, maps B on A. Since BA_b is perpendicular to BC which, in turn, is parallel to AD, the same rotation maps BA_b on AD and, similarly, BD on AB_a. It follows that the third sides of the triangles AB_aD and BDA_b are also mapped on each other. Thus the angle between them is 90°, as required.

Bottema's Theorem

1. Bottema's Theorem
2. An Elementary Proof of Bottema's Theorem
3. Bottema's Theorem - Proof Without Words
4. On Bottema's Shoulders
5. On Bottema's Shoulders II
6. On Bottema's Shoulders with a Ladder
7. Friendly Kiepert's Perspectors
8. Bottema Shatters Japan's Seclusion
9. Rotations in Disguise
10. Four Hinged Squares
11. Four Hinged Squares, Solution with Complex Numbers
12. Pythagoras' from Bottema's
13. A Degenerate Case of Bottema's Configuration
14. Properties of Flank Triangles
15. Analytic Proof of Bottema's Theorem

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2015 Alexander Bogomolny