Pythagoras' Theorem

Proof by Euclid

Euclid's proof hinges on two other Propositions from his Elements:

(VI.19) Similar triangles are to one another in the duplicate ratio of the corresponding sides.

(VI.20) Similar polygons are divided into similar triangles, and into triangles equal in multitude and in the same ratio as the wholes, and the polygon has to the polygon a ratio duplicate of that which the corresponding side has to the corresponding side.

So, if we have two shapes somehow related to a line segment, their areas change proportionally to the square of the line segment. Therefore, if, for a square, the area is a², for another shape related to a segment of length a, the area will be la², where the coefficient l depends on a particular shape. The general statement then claims that if three similar shapes were built on the sides of the right-angled triangle (a, b, c) then their areas would satisfy

la² + lb² = lc²

As we mentioned, Euclid has proven his statement for arbitrary polygons. Although the statement itself is more general, the identity it leads to is obviously equivalent to that asserted in a more traditional version of the Pythagoras' Theorem.

Thus, it could be said that, if the identity were to be shown in one particular case of similar shapes, it would follow for other shapes as well.

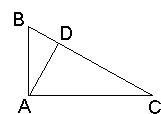
But one case is actually trivial. Consider similar triangles built on the sides of the given one. The one on the hypotenuse is simply the original triangle (see Proof #6). The other two lie on both sides of the altitude dropped from the right angle. That's it. (From a little different angle this argument is discussed elsewhere. [Schroeder, pp. 3-4], with a reference to reliable sources, mentions that this proof has been discovered by A. Einstein at the age of 11.)

Below is a Java applet demonstration of the Euclid's proof. Start dragging the mouse in a vicinity of the triangle. You'll see three similar triangles build on the sides of the original one. Drag the mouse into its right-angled corner.

Three numbers at the right near the bottom of the applet present areas of the three triangles. To compute the areas I actually used the Pythagorean Theorem itself and the Heron's formula

S² = p(p - a)(p - b)(p - c),

where p = (a + b + c)/2; a,b,c being the sides of a triangle with area S.

Besides the above, two particular configurations generated by the applet are especially suggestive. This is quite obvious that the areas of triangles 1 and 2 add up to that of triangle 3.

This one was pointed out by Scott Brodie. The small triangles just fold in to fill the big one.

Eli Maor [Maor, p. 116] thinks of this variant as the shortest possible proof of the Pythagorean Theorem. He points out that it is listed as the geometric proof 230 in Loomis' collection, where it's credited to Stanley Jashemski, age nineteen (1934), of Youngstone, Ohio.

(From a little different angle Euclid VI.31 is discussed elsewhere.)

References

1. E. S. Loomis, The Pythagorean Proposition, NCTM, 1968
2. E. Maor, The Pythagorean Theorem, Princeton University Press, 2007
3. M. Schroeder, Fractals, Chaos, Power Laws, Dover, 2009

|Up| |Contact| |Front page| |Contents| |Geometry| |Pythagorean Theorem|

Copyright © 1996-2018 Alexander Bogomolny