Bottema with a Product of Rotations
What Might This Be About?
Problem
Given $\Delta ABC$ and point $D,$ rotate $D$ clockwise around $B$ through angle $\alpha$ to obtain $D';$ rotate $D$ counterclockwise around $C$ by angle $\beta$ to obtain $D'';$ rotate $D''$ counterclockwise around $A$ through angle $\pi -\alpha -\beta$ to obtain $D'''.$ Let $E$ be the midpoint of $D'D'''.$
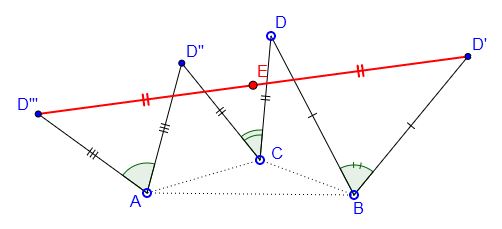
Prove that $E$ is independent of the position of $D.$
Solution
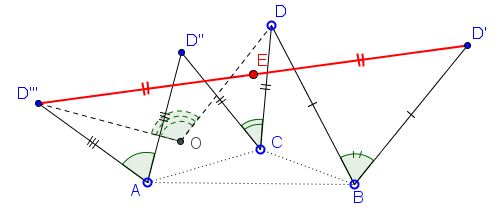
The product of two given rotations around $C$ and $A$ (one through angle $\beta,$ the other through angle $\pi -\alpha -\beta)$ is a rotation through angle $\beta + (\pi -\alpha -\beta)=\pi -\alpha,$ with the center denoted $O.$ This allows for an application of the generalized Bottema's theorem for the triangle $OBD.$
Acknowledgment
This problem is a follow-up of the one posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page, and a simple solution in complex numbers posted by Leo Giugiuc (Romania) and Leo's remark extending Dao's problem. Here's Dao's formulation:
Triangles $BET,$ $TAD,$ $DFC$ are similar isosceles. Prove that the midpoint $K$ of $EF$ is independent of the position of $D.$
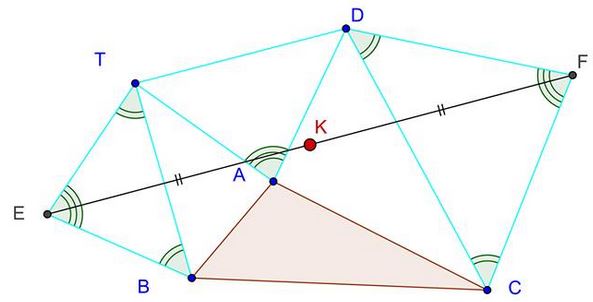
Following his solution, Leo observed that it applies to a more general case where the three triangle are just similar, not necessarily isosceles.
Note that the above statement generalizes Dao's formulation but not obviously Leo's that I placed in a separate file. Indeed, let $F'$ lie on $CF$ such that $CF'=CD;$ $E'$ on $BE$ such that $BE'=BT.$ (I refer here to Dao's diagram.) Than, by the above, the midpoint $K'$ of $E'F'$ is independent of the position of $D.$ Denoting $\displaystyle r=\frac{CF}{CF'}$ we observe that
$\displaystyle r=\frac{CF}{CF'} =\frac{CF}{CD}=\frac{BE}{BT}=\frac{BE}{BE'}.$
It thus follows that, if $\displaystyle K'=\frac{E'+F'}{2}$ is independent of $D,$ then so is
$\displaystyle \begin{align} K &= \frac{E+F}{2}\\ &=\frac{\big[B+(E-B)\big] + \big[C+(F-C)\big]}{2}\\ &=\frac{\big[B+r(E'-B)\big] + \big[C+r(F'-C)\big]}{2}\\ &=\frac{(1-r)(B+C)+r(E'+F')}{2}. \end{align}$
Bottema's Theorem
- Bottema's Theorem
- An Elementary Proof of Bottema's Theorem
- Bottema's Theorem - Proof Without Words
- On Bottema's Shoulders
- On Bottema's Shoulders II
- On Bottema's Shoulders with a Ladder
- Friendly Kiepert's Perspectors
- Bottema Shatters Japan's Seclusion
- Rotations in Disguise
- Four Hinged Squares
- Four Hinged Squares, Solution with Complex Numbers
- Pythagoras' from Bottema's
- A Degenerate Case of Bottema's Configuration
- Properties of Flank Triangles
- Analytic Proof of Bottema's Theorem
- Yet Another Generalization of Bottema's Theorem
- Bottema with a Product of Rotations
- Bottema with Similar Triangles
- Bottema in Three Rotations
- Bottema's Point Sibling
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572070
