Bottema in Three Rotations

Wojtek Wawrów
27 May, 2014

The following theorem and proof can be found in Waldermar Pompe's booklet Wokół obrotów (Theorem 3.5), and can be thought as of a generalization of a generalization of Bottema's theorem:

Given hexagon $ABCDEF$ (not necessarily convex) in which $AB=BC,$ $DC=DE,$ $FE=FA,$ let $\alpha,$ $\beta,$ $\gamma$ denote the internal angles of this hexagon at the vertices $B,$ $D,$ $F,$ respectively. Assume $\alpha +\beta +\gamma=360^{\circ}.$

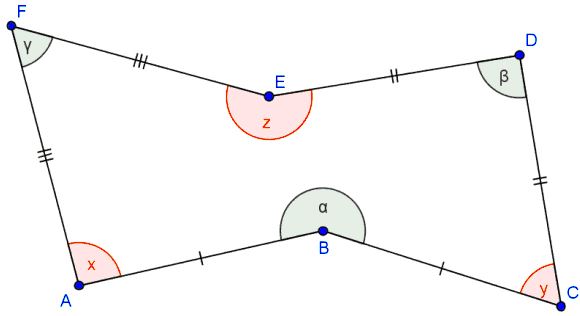
Bottema In Three Rotations - problem

Then at vertices $B,$ $D,$ $F,$ $\Delta BDF$ has angles $\displaystyle\frac{\alpha}{2},$ $\displaystyle\frac{\beta}{2},$ $\displaystyle\frac{\gamma}{2},$ respectively.

Proof

Let us also denote the other internal angles of hexagon as above. Note that because $\alpha +\beta +\gamma=360^{\circ}$ we also have $x+y+z=360^{\circ}.$ Thus there are two possibilities: either none exactly one of angles $x,y,z$ is at least $180^{\circ}.$ Without loss of generality assume $z\ge 180^{\circ}$ ((if none of the angles is concave, the argument won't change). Rotate $\Delta BCD$ around $D$ through angle $\beta$ so that point $C$ moves to point $E.$ Let $P$ be the image of point $B$ under this rotation. We can easily verify that $\angle PEF=x$ (because $\angle PED=y$ and $x+y+z=360^{\circ}.$Since we also have $PE=BC=AB$ and $EF=AF,$ we get $\Delta FAB=\Delta FEB.$ So, if we rotate $\Delta FAB$ around $F$ through angle $\gamma,$ we will get triangle $\Delta FEP.$

It follows that $BD=DP,$ $BF=PF,$ $\angle BDP=\beta,$ $\angle BFP=\gamma.$

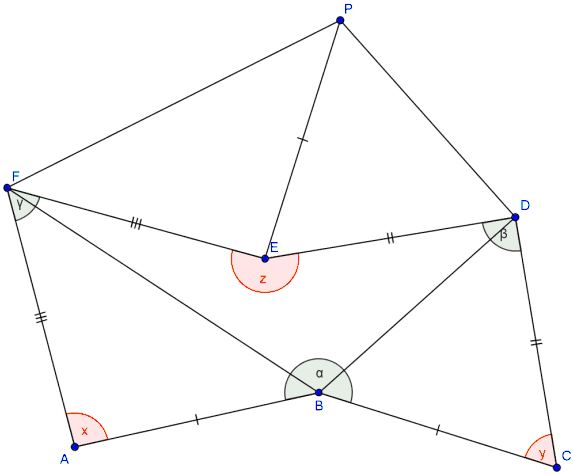
Bottema In Three Rotations - solution

Since $DBFP$ is a kite, diagonal $DF$ bisects two of its angles, giving us $\displaystyle\angle BDF=\frac{\beta}{2}$ and $\displaystyle\angle BFD=\frac{\gamma}{2}.$ That $\displaystyle\angle DFB=\frac{\alpha}{2}$ follows from $\alpha +\beta +\gamma=360^{\circ}.$

Now, how can this extend the generalization of Bottema's theorem? We'll show how this implies the generalized Bottema: apply above theorem to the hexagon $C_{B}DC_{A}ACB.$

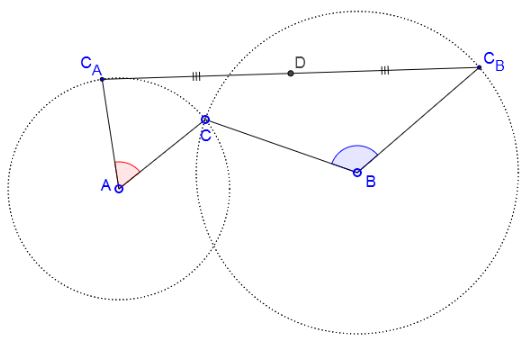
Bottema In Three Rotations leads to a genralization of generalization

Because $\angle C_{B}DC_{A}=180^{\circ},$ $\angle C_{A}AC+\angle CBC_{B}=180^{\circ}$ and $C_{B}D=DC_{A},$ $C_{A}A=AC,$ $CB=BC_{B},$ this is exactly the setup of the above theorem. So we instantly get $\displaystyle\angle ADB=\frac{180^{\circ}}{2}=90^{\circ}.$ We also get that angles $DAB$ and $DBA$ do not depend on point $C$ (because angles $CAC_A$ and $CBC_B$ don't depend on it) so the angles of $\Delta ABD$ don't depend on $C.$ Thus the only technicality we are left with is that, given angles of a triangle and one of its sides, the triangle can be "flipped" in two ways. But we can rule out the possibility of point $D$ "leaping" from one position to the other by considering continuous movement of point $C.$

Bottema's Theorem

  1. Bottema's Theorem
  2. An Elementary Proof of Bottema's Theorem
  3. Bottema's Theorem - Proof Without Words
  4. On Bottema's Shoulders
  5. On Bottema's Shoulders II
  6. On Bottema's Shoulders with a Ladder
  7. Friendly Kiepert's Perspectors
  8. Bottema Shatters Japan's Seclusion
  9. Rotations in Disguise
  10. Four Hinged Squares
  11. Four Hinged Squares, Solution with Complex Numbers
  12. Pythagoras' from Bottema's
  13. A Degenerate Case of Bottema's Configuration
  14. Properties of Flank Triangles
  15. Analytic Proof of Bottema's Theorem
  16. Yet Another Generalization of Bottema's Theorem
  17. Bottema with a Product of Rotations
  18. Bottema with Similar Triangles
  19. Bottema in Three Rotations
  20. Bottema's Point Sibling

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72187074