Property of Internal Angle Bisector - Hubert Shutrick's PWW
Let \(AD\) be an angle bisector in \(\Delta ABC\),
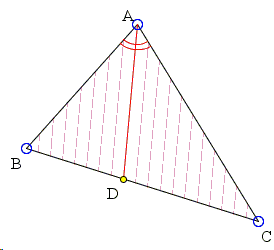
Then \(\displaystyle\frac{b}{c}=\frac{a_{b}}{a_{c}}\), where \(b=AC\), \(c=AB\), \(a_{b}=CD\), \(a_{c}=BD\).
(The applet below illustrates a proof by Hubert Shutrick. Points \(A\), \(B\), \(C\), \(A'\) are draggable.
Proof
This proof without words is due to Hubert Shutrick.
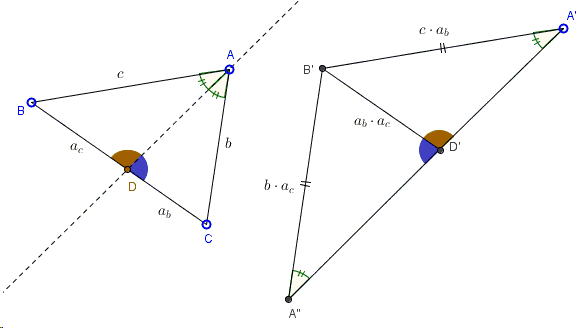
This is another example showing how the product identities that you get algebraically from similar triangles can be illustrated. The method applies in several additional situations.
(There are several theorems that are proved by similar technique.)
Angle Bisector
- Angle Bisector
- Angle Bisector Theorem
- All about angle bisectors
- Angle Bisectors in Ellipse
- Angle Bisectors in Ellipse II
- Angle Bisector in Equilateral Trapezoid
- Angle Bisector in Rectangle
- Property of Angle Bisectors
- Property of Angle Bisectors II
- A Property of Angle Bisectors III
- External Angle Bisectors
- Projections on Internal and External Angle Bisectors
- Angle Bisectors On Circumcircle
- Angle Bisectors in a Quadrilateral - Cyclic and Otherwise
- Problem: Angle Bisectors in a Quadrilateral
- Triangle From Angle Bisectors
- Property of Internal Angle Bisector - Hubert Shutrick's PWW
- Angle Bisectors Cross Circumcircle
- For Equality Choose Angle Bisector
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73579317
