For Equality Choose Angle Bisector
What Might This Be About?
Source
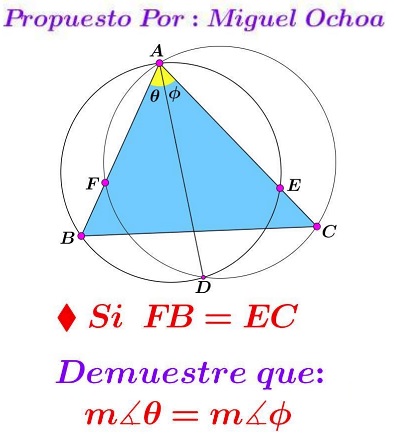
Problem
We'll prove a little more: the condition $BF=CE$ is not only sufficient for $\theta=\varphi,\;$ it is also necessary:
Given $\Delta ABC$ and point $D,$ on neither $AB$ or $AC.\;$ Form circles $(ABD)$ and $(ACD).$ Let $(ABD)$ intersect $AC$ in $E;\;$ $(ACD)$ intersect $AB$ in $F:$
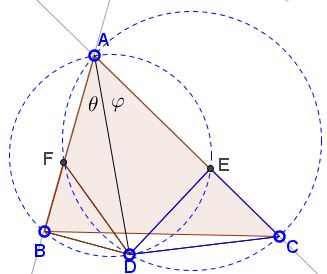
Let $\angle BAD=\theta,\;$ $\angle CAD=\varphi.\;$ Prove that $\theta =\varphi$ iff $BF=CE.$
Solution 1
Angles $\theta$ and $\varphi$ are subtended by the chords $BD,\;DE$ in circle $(ABD)$ and by the chords $DF,\;CD$ in circle $(ACD),$ implying $\displaystyle\frac{DF}{CD}=\frac{BD}{DE}.\;$ In addition, $\angle BDF=\angle BDE-\angle FDE,$ whereas $\angle CDE=\angle CDF-\angle FDE.\;$ But both angles $BDE$ and $CDF$ are supplementary to $\angle BAC$ and are thus equal. It follows that $\angle BDF=\angle CDE,\;$ and, consequently, triangles $BDF$ and $CDE$ are similar. They are equal when, say, the two chords $BD\;$ and $DE\;$ in circle $(ABD)\;$ are equal. This only happens when $\theta=\varphi.$ Thus $\Delta BDF=\Delta CDE\;$ and then also $BF=CE\;$ iff $AD$ bisects $\angle BAC.$
Solution 2
Here we establish only the sufficiency of the condition $BF=CE\;$ for $\theta=\varphi.\;$ Introduce $M,N,P,\;$ and $x$ as below.
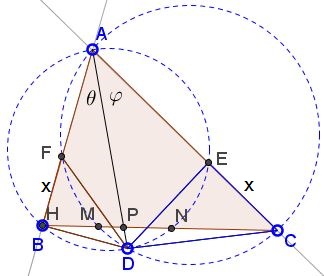
Denote circle $(ABE)\;$ as $w\;$ and circle $(ACF)\;$ as $q.\;$ By the power of B relative to $q,\;$ $BM\cdot BC=BF\cdot AB,$ i.e., $a\cdot BM=xc.\;$ SImilarly, by the power of $C$ with respect to $w,\;$ $a\cdot CN=x\cdot b.$ From here, $\displaystyle\frac{BM}{CN}=\frac{c}{b}.$
$P$ belongs to the radical axis of $w\;$ and $q,\;$ hence, it has the same power relative to both $w\;$ and $q.\;$ It follows that $PB\cdot PN=PC\cdot PM,\;$ or, $PB(PC-CN)=PC(PB-BM),\;$ which is equivalent to $PB\cdot CN=PC\cdot BM,$ implying $\displaystyle\frac{PB}{PC}=\frac{BM}{CN}=\frac{c}{b}.$ By the inverse of the Internal Bisector theorem, $AP\;$ is the angle bisector of $\angle BAC.$
Acknowledgment
The problem that is due to Miguel Ochoa Sanchez has been posted by Leo Giugiuc at the CutTheKnotMath facebook page along with a solution (Solution 2) by Leo Giugiuc and Dan Sitaru.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73615330
