Angle Bisector Theorem

Angle bisectors in a triangle have a characteristic property of dividing the opposite side in the ratio of the adjacent sides. More accurately,

Let AD - with D on BC - be the bisector of ∠A in ΔABC. If b = AC, c = AB, m = CD, and n = BD, then

b/c = m/n.

Jelena Nikolin from Serbia has graceously supplied several proofs. Below, (Δ) denotes the area of triangle Δ.

Proof 1

Here is a proof that does not appeal to the similarity of triangles. Instead, we'll argue that

(ACD) : (ABD) = m : n,

because the two triangles share the altitude from A.

On the other hand, point D is equidistant from the sides b and c (it belongs to the angle bisector), so altitudes of the smaller triangles from D are equals. These are denoted h:

(ACD) : (ABD) = bh/2 : ch/2 = b : c,

implying m : n = b : c.

Proof 2

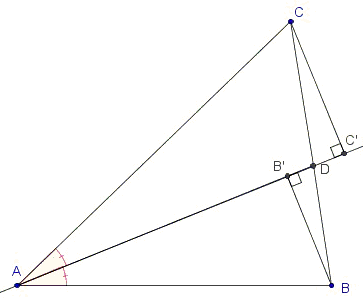
Let B' and C' are foots of the perpendicular from B and C to the angle bisector. Triangles ABB' and ACC' are similar - the two are right and have equal acute angles at A. So

AB : AC = BB' : CC'. (*)

Further, triangles BB'D and CC'D are similar too so

BB' : CC' = BD : CD. (**)

From (*) and (**) we have AB : AC = BD : CD.

Remark: These two proofs are not original, but do have educational value.

Proof 3

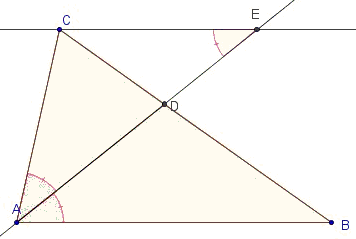
Let E be the intersection of AD and the line parallel to AB through C. ∠AEC = ∠BAE (Transversal theorem: the line that cuts two parallels, cuts it under equal angles), meaning that ΔACE is isosceles and thus AC = CE. In addition, triangles ABD and ECD are similar, implying

AB : CE = BD : CD.

Together with CE = AC, we obtain the required AB : AC = BD : CD.

Proof 4

This proof is based on the following lemma that is of interest in its own right:

Let B' is the point on the segment AC where B'D||AB. Let C' is point on the segment AB such that C'D||AC. Then AB'DC' is a rhombus.

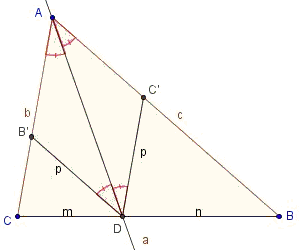
Proof of Lemma

∠DAC = ∠ADC' = ∠DAB = ∠ADB' = α/2 (transversal). Now, triangles ADB' and ADC' are congruent by ASA, so B'D = C'D = p. Since quadrilateral AB'DC' is a parallelogram with each sides equal, it is a rhombus.

Using Thales' theorem, we have: B'D : AB = CD : BC or

p : c = m : a (*)

and C'D : AC = BD : BC, or

p : b = n : a (**).

Combining (*) and (**), we end up with m : n = b : c.


Related material
Read more...

Angle Bisector

  • Angle Bisector
  • All about angle bisectors
  • Angle Bisectors in Ellipse
  • Angle Bisectors in Ellipse II
  • Angle Bisector in Equilateral Trapezoid
  • Angle Bisector in Rectangle
  • Property of Angle Bisectors
  • Property of Angle Bisectors II
  • A Property of Angle Bisectors III
  • External Angle Bisectors
  • Projections on Internal and External Angle Bisectors
  • Angle Bisectors On Circumcircle
  • Angle Bisectors in a Quadrilateral - Cyclic and Otherwise
  • Problem: Angle Bisectors in a Quadrilateral
  • Triangle From Angle Bisectors
  • Property of Internal Angle Bisector - Hubert Shutrick's PWW
  • Angle Bisectors Cross Circumcircle
  • For Equality Choose Angle Bisector

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71946060