Angle Bisectors in a Quadrilateral
Cyclic and Otherwise

What is this about?
A Mathematical Droodle

Explanation

Related material
Read more...

Angle Bisector

  • Angle Bisector
  • Angle Bisector Theorem
  • All about angle bisectors
  • Angle Bisectors in Ellipse
  • Angle Bisectors in Ellipse II
  • Angle Bisector in Equilateral Trapezoid
  • Angle Bisector in Rectangle
  • Property of Angle Bisectors
  • Property of Angle Bisectors II
  • A Property of Angle Bisectors III
  • External Angle Bisectors
  • Projections on Internal and External Angle Bisectors
  • Angle Bisectors On Circumcircle
  • Problem: Angle Bisectors in a Quadrilateral
  • Triangle From Angle Bisectors
  • Property of Internal Angle Bisector - Hubert Shutrick's PWW
  • Angle Bisectors Cross Circumcircle
  • For Equality Choose Angle Bisector

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    The applet attempts to suggest the following problem:

    In quadrilateral ABCD, define X as the intersection of bisectors of angles CAD and CBD, and Y as the intersection of the bisectors of angles ACB and ADB. Also, let U, V, G be the intersections of AX,DY; BX,CY; AC,BD, respectively.

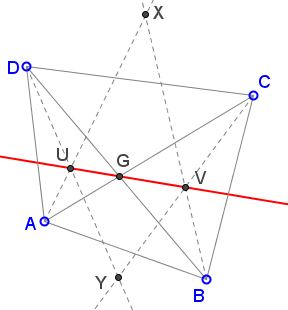
    Angle bisectors in quadrilateral - problem

    Prove that

    1. U, G, V are collinear.
    2. If ABCD is cyclic then X and Y lie on its circumcircle.

    (The problem is rather straightforward. It's an attempt to salvage time spent on verifying the faulty formulation of an olympiad problem that appears online. This is problem #10.2 from the 1994-1995 Regional St Petersburg Mathematical Olympiad. The formulation as it stands is definitely wrong.)

    U and V are the incenters of triangles ADG and BCG, such that GU and GV are their third angles bisectors. GU and GV bisect two vertical angles and therefore form a straight line.

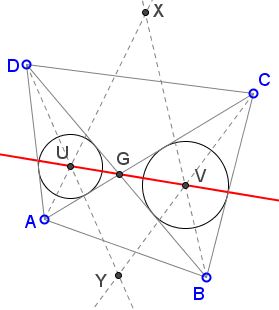
    Angle bisectors in quadrilateral - solution

    When ABCD is cyclic, the bisector of ∠CAD meets the circumcircle of ABCD the second time at the midpoint of arc CD. The same holds for the bisector of ∠CBD. Thus the two intersect (at point X) on the circumcircle. Point Y is treated similarly.

    It is possible to formulate a less trivial problem by making away with the requirement of the cyclicity of the quadrilateral:

    In quadrilateral ABCD, define X as the intersection of bisectors of angles CAD and CBD, and Y as the intersection of the bisectors of angles ACB and ADB. Then, if X lies on the circumcircle of ΔBCD, then so does Y.

    For a proof, observe that X lies on the circumcircle of ΔBCD iff A lies on that circle. Indeed, let C(BCD) and C(ACD) be the circumcircles of triangles BCD and ACD respectively. The bisector of ∠BCD meets C(BCD) in, say, X', and that of ∠ACD meets C(ACD) in X''. The two points coincide iff they both lie on the circumcircle of triangle X'(X'')CD. Which means that C(BCD) = C(ACD), so that A∈C(BCD).

    But this makes the quadrilateral ABCD cyclic and we may now reuse the previous result.

    |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72258626