Angle Bisectors Cross Circumcircle
Problem
Let $I$ be the incenter of $\Delta ABC$ and points $A', B', C'$ the intersections of the extended angle bisectors $AI,BI,CI$ with the circumcircle of the triangle.
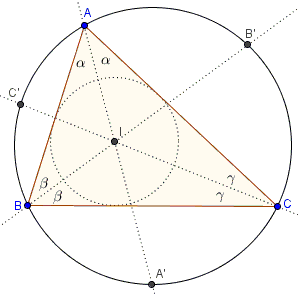
Prove that
$\displaystyle\frac{IA'\cdot IC'}{IB}=R$ and
$\displaystyle\frac{IA\cdot IC}{IB'}=2r,$
where $R$ is the circumradius, $r$ the inradius, of $\Delta ABC.$
Hint
I do not know if you can do that without using some trigonometric identities in a triangle. Also, having intersecting chords in a circle brings to mind a certain well-known theorem.
Solution

According to the Intersecting Chords theorem, say, $IA\cdot IA' = IB\cdot IB' = IC\cdot IC',$ implying
$\displaystyle\frac{IA'\cdot IC'}{IB}=\frac{IB'\cdot IC'}{IA}.$
Similarly,
$\displaystyle\frac{IA'\cdot IC'}{IB}=\frac{IB'\cdot IC'}{IA}=\frac{IA'\cdot IB'}{IC}$
and
$\displaystyle\frac{IA\cdot IC}{IB'}=\frac{IB\cdot IC}{IA'}=\frac{IA\cdot IB}{IC'}.$
It follows that what we have to prove is equivalent to
$\displaystyle\frac{(IA'\cdot IB'\cdot IC')^2}{IA\cdot IB\cdot IC}=R^3$
and
$\displaystyle\frac{(IA\cdot IB\cdot IC)^2}{IA'\cdot IB'\cdot IC'}=(2r)^3.$
Let $\angle A=2\alpha,$ $\angle B=2\beta,$ and $\angle C=2\gamma.$ By the Sine Law,
$\displaystyle\frac{IA}{AC}=\frac{\mbox{sin}\gamma}{\mbox{sin}(\pi -\alpha -\gamma)}=\frac{\mbox{sin}\gamma}{\mbox{cos}\beta}.$
In other words, $\displaystyle IA=b\cdot\frac{\mbox{sin}\gamma}{\mbox{cos}\beta}.$
Similarly, $\displaystyle IB=c\cdot\frac{\mbox{sin}\alpha}{\mbox{cos}\gamma}$ and $\displaystyle IC=b\cdot\frac{\mbox{sin}\beta}{\mbox{cos}\alpha}.$
Now note that $\angle IAB'=\alpha+\beta=\angle AIB',$ making $\Delta AB'I$ isosceles so that $AB'=IB'.$ It follows that $\displaystyle\frac{IB'}{AB}=\frac{AB'}{AB}=\frac{\mbox{sin}\beta}{\mbox{sin}2\gamma}.$ In other words, $\displaystyle IB'=c\frac{\mbox{sin}\beta}{\mbox{sin}2\gamma}.$ Similarly, $\displaystyle IC'=a\frac{\mbox{sin}\gamma}{\mbox{sin}2\alpha}$ and $\displaystyle IA'=b\frac{\mbox{sin}\alpha}{\mbox{sin}2\beta}.$
Multiplying what we got so far,
$\displaystyle IA\cdot IB\cdot IC=abc\frac{\mbox{sin}\alpha\cdot\mbox{sin}\beta\cdot\mbox{sin}\gamma}{\mbox{cos}\alpha\cdot\mbox{cos}\beta\cdot\mbox{cos}\gamma}$
and
$\displaystyle IA'\cdot IB'\cdot IC' =abc\frac{\mbox{sin}\alpha\cdot\mbox{sin}\beta\cdot\mbox{sin}\gamma}{\mbox{sin}2\alpha\cdot\mbox{sin}2\beta\cdot\mbox{sin}2\gamma}.$
From the double argument formulas,
$\displaystyle \frac{\mbox{sin}^{2}\alpha}{\mbox{sin}^{2}2\alpha}\cdot\frac{\mbox{cos}\alpha}{\mbox{sin}\alpha}=\frac{1}{2\mbox{sin}2\alpha}$
and
$\displaystyle \frac{\mbox{sin}2\alpha}{\mbox{sin}\alpha}\cdot\frac{\mbox{sin}^{2}\alpha}{\mbox{cos}^{2}\alpha}=\frac{2\mbox{sin}^{2}\alpha}{\mbox{cos}\alpha}$
all that remains is to check that
$\displaystyle R^{3}=\frac{abc}{8\mbox{sin}2\alpha\cdot\mbox{sin}2\beta\cdot\mbox{sin}2\gamma}$
and
$\displaystyle 8r^{3}=\frac{8\space {abc}\mbox{sin}^{2}\alpha\cdot\mbox{sin}^{2}\beta\cdot\mbox{sin}^{2}\gamma}{\mbox{cos}\alpha\cdot\mbox{cos}\beta\cdot\mbox{cos}\gamma}.$
But the first identity follows from the law of sines:
$\displaystyle 2R=\frac{a}{\mbox{sin}\alpha}=\frac{b}{\mbox{sin}\beta}=\frac{c}{\mbox{sin}\gamma}$
while the second one is a consequence of
$\displaystyle r=IA\cdot\mbox{sin}\alpha=b\frac{\mbox{sin}\alpha\cdot\mbox{sin}\gamma}{\mbox{cos}\beta}=a\frac{\mbox{sin}\beta\cdot\mbox{sin}\gamma}{\mbox{cos}\alpha}=c\frac{\mbox{sin}\alpha\cdot\mbox{sin}\beta}{\mbox{cos}\gamma}.$
Acknowledgment
This is problem 11.7 from V. V. Prasolov's Problems in Planimetry (v 1, Nauka, Moscow, 1986 (Russian).)
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572533
