Twelve Matchsticks Area Puzzle
Twelve matches can be arranged to form a cross - a shape whose area is obviously 5 match2, so to speak, or just 5, if we think of the length of a matchstick as a unit of length.
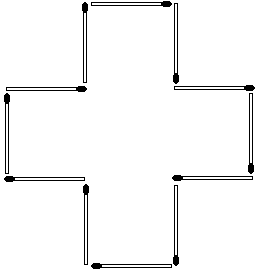
Question: are there shapes formed by (whose boundary consists of) 12 matchsticks with area 4, 3 or even 2?
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyTwelve matches can be arranged to form a cross - a shape whose area is obviously 5 match2, so to speak, or just 5, if we think of the length of a matchstick as a unit of length.

Question: are there shapes formed by (whose boundary consists of) 12 matchsticks with area 4, 3 or even 2?
The answer is yes; and, for those acquainted with the Pythagorean theorem, it is easy to see why this is so.
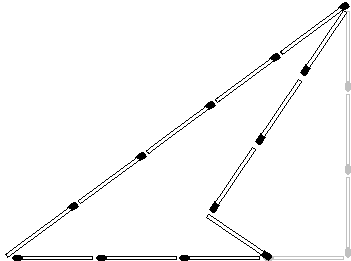
Among many triangles with perimeter 12, the most famous is the 3-4-5 triangle, the triangle with sides 3, 4, and 5 (or a similar one.) Since

The right triangle with sides 3 and 4 has area of

of area 5,

and of area 4 (this is appears in [Gardner, p. 120]),

and finally one of area 3, too.
But then what is one, unaware of the Pythagorean theorem, supposed to do? The above solution that relies on the knowledge of the theorem may suggest that the problem is too advanced. One of my young relatives - a 7 years old Sam Zbarsky - came up with an ingenious solution that only uses an intuitive idea of a number not being changed after addition and subsequent subtraction of the same quantity. The number in question is 4, the area of a T-shaped region obtained from the cross by removing one of the squares. The quantity added and subtracted is the area of an equilateral triangle formed by three matchsticks. Note that the solution does not really require knowledge of the formula for the area of a triangle, nor the numeric value of the area of the specific triangle at hand.

The same addition/subtraction of equilateral triangles applied to the remaining two sides of the original cross produce a shape of area 3:

Now, there is a third way for making a shape of area 3? Can you find it?
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnySolution (Area of 3)
It should be easy now to come up with a shape of area 2, right?
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnySolution (Area of 2)

Here is a point worth noticing. We may start with a 3×3 square of area 9 and folding in a square at a time get the shapes of areas 8, 7, and 6. The cross this page starts with is only one of several possible shapes with area of 5. One of these is a rectangle 1×5. The rectangle can be flattened into a parallelogram of arbitrary small area. I doubt that this is an acceptable solution unless we know how to determine its height. This is possible, e.g., when the height is the altitude of the regular triangle: √3/2.
But what is the largest area that could be enclosed with 12 matches? It must be the area of the regular dodecagon (12-gon). If only you can draw a proper circle ...
(Talking of areas, you know it takes 14 matches to make a square. The 3:4:5 triangle makes unexpected multiple appearances in a folded square paper and no less surprisingly leads to a Golden Ratio.)
References
- M. Gardner, Hexaflexagons and Other Mathematical Diversions, The University of Chicago Press, 1988
- N. Yoshigahara, Puzzles 101, A K Peters, 2004
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73607751
