Angle Trisection by Hippocrates

Hippocrates (470-410 B.C.) of Chios, famous for his work on quadrature of circular lunes and the arrangement of theorems in a logical manner, later used by Euclid in his Elements, also left the first known construction for the trisection of an angle. As the trisection of Archimedes, this one, too, is not done by straightedge and compass, which we know is impossible. (Such constructions that employ tools beyond straightedge and compass are known as neusis constructions. We also have a 21^st century construction which serves to show that some problems in mathematics never lose their appeal.) Hippocrates of Chios, a mathematician and astronomer, should not be confused with the physician Hippocrates of Cos (460-ca. 370 B.C.), whom we owe the Oath of Hippocrates.

For a given angle BAC, let D be the foot of the perpendicular from C to AB. Form a rectangle ADCF and extend CF beyond C. On the extension we shall place an additional point E. If H is the intersection of AE and CD, then E is chosen so as to satisfy

When this is done, the angle BAE is one third the angle BAC.

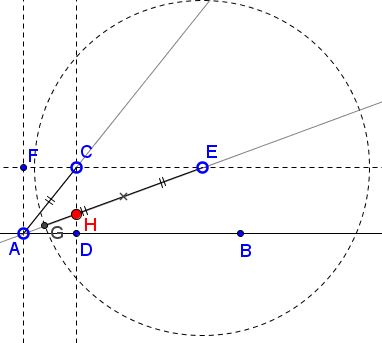
The proof is hinted at by the applet. Let G be the midpoint of EH. Since CGE is isosceles (CG being the median to the hypotenuse of the right triangle CEG), the angles ECG and GEC are equal. The external angle AGC is twice as large. ACG is also isosceles,

CAG = AGC.

Finally, the angles AEC and BAE are alternate interior angles (CE||AB and AE a transversal), they are thus equal, which gives

CAE = 2·BAE.

Remark (July 2007)

This page has been written in March 2005. In June 2007 I received a letter that in particular offered a solution to the trisection problem. Having written a page outlining that solution I thought it might be a good idea to describe other attempts at the angle trisection. I began with ordering U. Dudley's book on trisectors and reviewing the pages on that topic I have already written. Dudley introduces the above method on p. 5 with a references to an 1907 article in the American Mathematical Monthly as an improvement on Archimedes' method. However, Archimedes is about 200 years younger than Hippocrates and had to be aware of the above solution. Thus, assuming (1) that the solution is Hippocrates' and (2) that it was known to Archimedes, the characterization as "improvement" which suggests a reversed time sequence of events caught my attention.

Upon checking the current page for a reference, I have discovered to my horror that no such reference has been given. As of this writing, I failed to locate a proper reference that identifies Hippocrates as the author of the construction except for an online source. However, the construction has been already known to Puppus as he mentions it in his commentaries.

I'll continue looking for a reference that identifies Hippocrates as the author of the construction. I'll appreciate any help with this endeavor.

References

1. U. Dudley, The Trisectors, MAA, 1994
2. I. Thomas, Greek Mathematical Works, v. 1, Harvard University Press, 2006, 353-355
3. E. E. White, On the Trisection of an Angle, Am Math Monthly, Vol. 14, No. 8/9. (Aug. - Sep., 1907), pp. 151-152.

Copyright © 1996-2008 Alexander Bogomolny