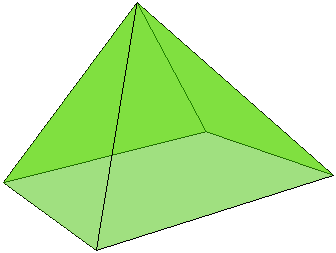
Stuart Anderson has posed the question of comparing the volumes V of a tetrahedron (3-pyramid) and W of a square pyramid (4-pyramid), with all 14 edges they have between them equal. What do you think is the relationship between V and W?
We shall show that W = 2V.
Solution 1
Assuming that the length of the common edges is 1, V = √2/12, whereas W = √2/6, so that 2V = W. Calculations are not difficult. The volume of a pyramid equals 1/3 of the altitude times the area of the base.
The altitude of a square pyramid is the altitude in an isosceles triangle with sides √3/2, √3/2, 1, which is √2/2. W = 1/3×√2/2×1 = √2/6.
The altitude of a regular tetrahedron, is the altitude to the side of the isosceles triangle with sides √3/2, √3/2, 1, which is √6/3. V = 1/3×√6/3×√3/4, the latter factor being the area of the unit equilateral triangle. Thus V = √2/12.
Solution 2
By Stuart Anderson.
Let the bases of the pyramids tile the plane with squares, draw a second plane through the apices of the pyramids, and let a second set of inverted pyramids tile this plane with their bases, the corners of each base coinciding with the apices of the upright pyramids. Since the volume of a pyramid is 1/3·h·(base area), while the volume of a rectangular slab is h·(base area), the pyramids together fill 2/3 of the volume of the slab. The spaces between the pyramids are rather obviously perfect regular tetrahedrons, and since each of these shares a face with 4 pyramids, while each upright pyramid shares a face with 4 tetrahedrons, they are equinumerous. Hence, since they are equal in number and fill the remaining 1/3 of the volume, their individual volumes must be in the inverse proportion: W:V = (2/3):(1/3), or W = 2V.
Solution 3
It's a well known curiosity that the faces of 3- and 4-pyramids align when adjacent faces are glued together.
Let's start with just four 4-pyramids whose bases form a square. The space between any successive two can be filled with a 3-pyramid by joining their apices. These four lines form a base of an inverted 4-pyramid and, if we put one more 4-pyramid on top of that base, we'll get a 4-pyramid twice the size of the original one (and 8 times the volume.) This big 4-pyramid consists of 6 small 4-pyramids and four 3-pyramids, implying
8W = 6W + 4V,
so that W = 2V. (This solution is accompanied by an interactive illustration.)
Solution 4
This solution is due to Matt Henderson.
Draw the midlines of the faces of a regular tetrahedron. This operation shows 4 tetrahedra - one at each of the four vertices of the original tetrahedron. What remains if the small tetrahedra is cut off is a regular octahedron, the shape that consists of two square pyramids laid base-to-base. (Check a dynamic illustration.) This we get the equation
8V = 4V + 2W,
or, 4V = 2W, and, finally, W = 2V, as before.
